Créer et exécuter un modèle PLS-PM simple

Le principe de l’approche PLS

L’approche PLS est une méthode statistique permettant de modéliser des relations complexes entre des variables observées et des variables latentes. Ce type de modèles est généralement appelé modèle d’équations structurelles à variables latentes.

Depuis quelques années, cette approche est de plus en plus populaire dans des communautés scientifiques très variées (Esposito Vinzi et al., 2007). Les modèles d’équations structurelles (Structural Equation Models) comprennent un grand nombre de méthodologies statistiques (dont l’approche PLS fait partie) qui permettent l’estimation de relation de causalité complexes entre des variables latentes mesurées elles-mêmes par des variables observées dites manifestes.

L’approche PLS dans sa version actuelle a été présentée pour la première fois par Herman Wold en 1979, mais les articles de référence sur cette méthode sont Wold (1982 et 1985).

Du point de vue classique des modèles d’équations structurelles à variables latentes, l’approche PLS est une méthode basée sur des composantes pour laquelle la causalité est formulée en termes d’espérance conditionnelle linéaire.

L’approche PLS privilégie la recherche d’une optimalité prédictive des relations plutôt que celle de relations de causalité. Elle est orientée de manière prédictive afin de tester des hypothèses de causalité. Ainsi, plutôt que de valider un modèle en termes de qualité d’ajustement, on utilisera des indices de qualité prédictive. Pour plus de détails sur ces points, on peut voir l’aide de XLSTAT et deux articles de référence sur le sujet : Chin (1998, plutôt orienté vers les applications) et Tenenhaus et al. (2005, plutôt orienté vers la théorie).

Par ailleurs, l’approche PLS permet d’analyser des tableaux multiples et peut être directement reliée à des méthodes d’analyse de données classiques de ce domaine. En fait, l’approche PLS peut aussi être vue comme une méthode extrêmement flexible dans l’analyse de tableaux multiples grâce à , d’une part, l’approche PLS hiérarchique et, d’autre part, l’approche PLS confirmatoire (Tenenhaus et Hanafi, 2007). Ces approches montrent que les méthodes classiques basées sur les données (« data-driven methods ») peuvent être reliées à des méthodes basées sur la théorie (« theory-driven methods ») telle que les modèles d’équations structurelles. Ceci permet d’intégrer des connaissances sur les relations entre les tableaux dans les analyses.

L’approche PLS avec XLSTAT-PLSPM

Dans ce tutoriel, nous vous guidons afin de créer un projet, définir un modèle, estimer les paramètres de celui-ci et analyser les résultats. Ce tutoriel est basé sur l’article suivant : [Tenenhaus M., Esposito Vinzi V., Chatelin Y.-M. and Lauro C. (2005). PLS Path Modeling. Computational Statistics & Data Analysis, 48(1), 159-205].

L’application présentée est basée sur des données réelles. 250 clients d’un opérateur de téléphones portables ont été contactés afin de répondre à un grand nombre de questions pour pouvoir modéliser leur fidélité envers l’opérateur. Le modèle PLSPM est basé sur l’indice de satisfaction européen des clients (ECSI). Ce modèle à variables latentes est représenté dans la figure suivante :

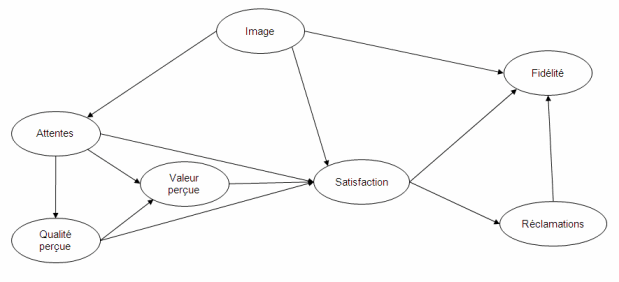
Chaque variable latente est reliée à un certain nombre de variables manifestes qui sont directement observables et donc mesurées. Dans cette application, les variables manifestes sont mesurées sur des échelles de 0 à 100. Par exemple, pour la variable latente image, les cinq variables manifestes associées sont :

• on peut avoir confiance en ce qu’il fait et dit
• c’est un opérateur stable et bien implanté
• c’est un opérateur qui apporte une contribution sociale à notre société
• c’est un opérateur pour lequel les clients sont importants
• c’est un opérateur innovant

Jeu de données pour appliquer l’approche PLS

Les projets XLSTAT-PLSPM sont des classeurs Excel spécifiques. Lorsqu’un nouveau projet est créé, il prend le nom PLSPMBook. Il est possible ensuite de le sauver, mais il faut bien utiliser la commande de sauvegarde de la barre XLSTAT-PLSPM afin de la sauvegarder en entier avec l’extension *.ppmx.

Note : il peut arriver que lorsqu’on ouvre le fichier, l’affichage soit mal organisé. Il suffit de cliquer sur « Optimiser l’affichage » (voir plus loin).

Un projet XLSTAT-PLSPM vierge contient deux feuilles qui ne peuvent pas être supprimées : - D1 : feuille de calcul vide dans laquelle il faut copier les données que l’on veut traiter. - PLSPMGraph : Feuille blanche utilisée pour dessiner le modèle. Lorsque cette feuille est sélectionnée, la barre d’outils apparaît.

Dans le cadre de ce tutoriel, afin de créer le projet on doit utiliser les fonctions PLSPM :

L’approche PLS étant une méthode statistique complexe et les développements présents dans le module PLSPM étant très développés, nous avons mis en place deux types d’affichage des menus. Un premier, paramétré par défaut et rassemblant les principales fonctions associées à l’approche PLS, appelé « classique » et un second permettant des recherches plus avancées appelé « expert ». Pour modifier cette option, cliquer sur le bouton options PLSPM :

Dans le cadre de ce tutoriel, nous nous focaliserons sur l’affichage classique qui permet d’appliquer l’approche PLS dans les cas généraux. Nous sauvons maintenant le projet en utilisant la fonction « enregistrer le projet sous ».

Attention, il faut toujours sauvegarder et ouvrir les projets .ppmx en utilisant les fonctions PLSPM et non les fonctions classiques d’Excel.

Nous copions les données d’une feuille classique Excel vers la feuille D1. On peut alors mettre en place le modèle. Allez vers la feuille PLSPMGraph. La barre de commandes se trouve en haut à gauche :

Afin de créer plusieurs variables latentes à la suite, double-cliquez sur le bouton dédié, de façon à ce qu’il reste enfoncé :

Vous pouvez alors ajouter les flèches reliant les variables latentes les unes aux autres. Pour ajouter une flèche, il suffit de cliquer sur la variable latente de laquelle elle part et de sélectionner la variable latente de destination en gardant appuyer le bouton CtrL. Une fois les deux variables sélectionnées, utilisez soit le bouton de la barre d’outil comme dans la figure suivante, soit le raccourci clavier Ctrl+L.

Une fois que tous les liens ont été ajoutés, il faut définir les variables manifestes associées à chaque variable latente. La manière la plus rapide consiste à cliquer sur la variable latente et utilisez le bouton MV de la barre :

Ceci active une boîte de dialogue qui s’ouvre sur la feuille D1. Cette boîte permet de donner un nom à la variable latente, définir les variables manifestes et mettre en place quelques options de base.

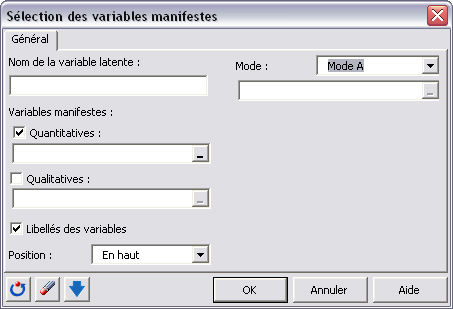
Ce menu permet de définir chacun des blocs de variables manifestes en sélectionnant les données dans la feuille de calcul D1. On doit aussi choisir le mode d’estimation : dans le cadre de cette application nous supposons que les construit sont réflectifs et sélectionnons donc le mode A. Dans le mode A, les variables manifestes sont des reflets de la variable latente, c’est le cas réflectif. Dans le mode B, les variables manifestes construisent la variable latente, c’est le cas formatif.

Par exemple, pour la variable latente Attente, la boîte de dialogue aura la forme suivante :

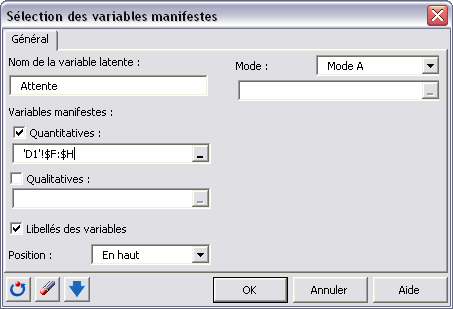
Le modèle obtenu a la forme suivante :

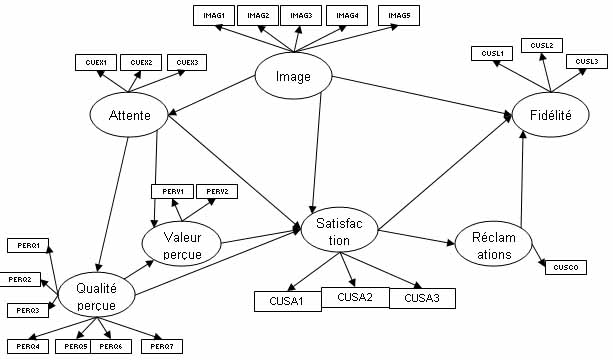
Une fois l’ensemble du modèle construit, on peut lancer l’application de l’approche PLS en utilisant la barre d’outils et en cliquant sur "Lancer les calculs" :

La boîte de dialogue « lancer les calculs » apparaît :

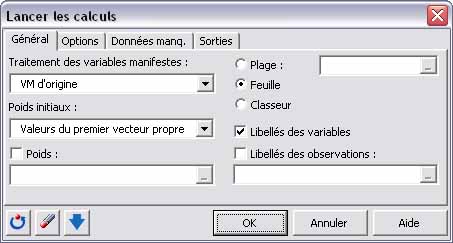
Dans notre application, les variables manifestes ayant toutes les mêmes échelles, on peut travailler sur les données d’origine (il existe 4 alternatives). L’algorithme PLS (décrit dans l’aide XLSTAT) doit être initialisé, on choisit ici comme vecteur d’initialisation des poids externes les valeurs du premier vecteur propre issues d’une analyse en composantes principales sur chaque bloc (il existe 2 alternatives).

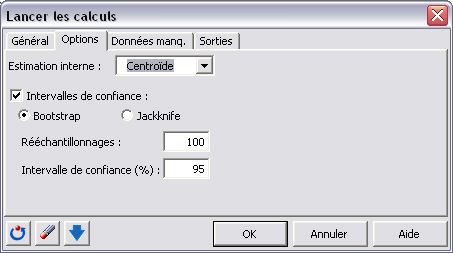
L’onglet « options » permet de choisir le schéma d’estimation des poids. Dans le cadre de cette application, nous utilisons le schéma centroïde. Nous utilisons le bootstrap afin d’obtenir des intervalles de confiance.

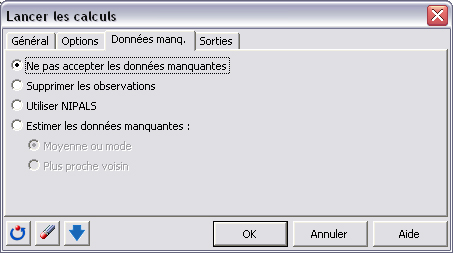
L’onglet « données manq. » n’est pas modifié car aucune données n’est manquante dans le jeu de données traité. Néanmoins, XLSTAT-PLSPM permet d’utiliser de nombreuses méthodes de traitement des données manquantes dont l’algorithme NIPALS qui est spécifique à l’approche PLS. Ces méthodes sont détaillées dans l’aide de XLSTAT.

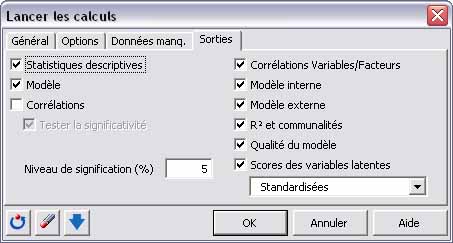
Finalement, l’onglet “Sorties” permet de choisir les résultats que l’on désire afficher dans le feuille des sorties. Nous détaillerons ces résultats dans la partie suivante.

Résultats et interprétation des sorties d’un projet PLSPM

La première partie des résultats rassemble des informations sur les données et le modèle créé (statistiques descriptives des variables manifestes, spécification du modèle).

Le premier élément important est la vérification de l’unidimensionnalité des blocs. Nous nous trouvons dans le cas réflectif, les blocs doivent donc être unidimensionnels. On utilise donc le tableau donnant la fiabilité des blocs :

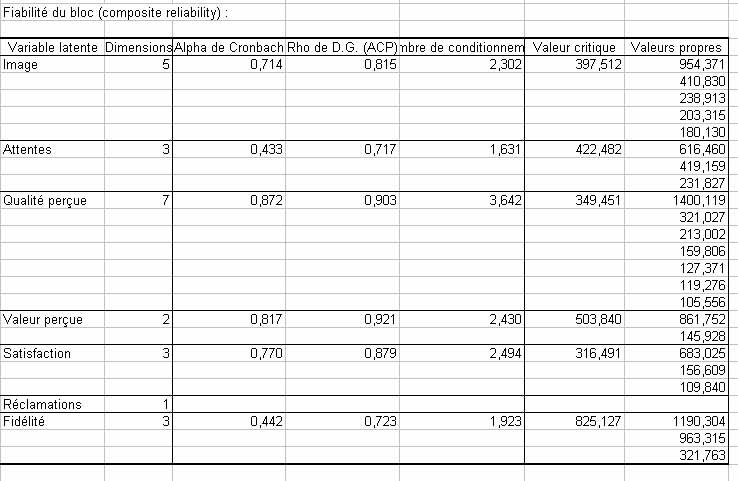
On peut voir que l’alpha de Cronbach est en-dessous de son seuil pour les variables Attente et Fidélité. Néanmoins, le rho de Dillon et Goldstein est toujours supérieur à 0,7. Finalement, la première valeur propre est beaucoup plus grande que la seconde dans beaucoup de cas. Ces résultats nous poussent à considérer que les blocs sont unidimensionnels même si une analyse des dimensions supplémentaires de l’attente et de la fidélité pourrait être intéressante. Par ailleurs, les indices n’apparaissent pas pour la variable latente Réclamations car elle ne possède qu’une seule variable manifeste associée.

Afin d’aller plus loin dans la recherche de dimensions supplémentaires, XLSTAT donne des tableaux de corrélations pour chaque variable latente entre les variables manifestes et les facteurs obtenus par une ACP sur chaque bloc. Dans le cadre de cette application, nous nous focalisons sur une seule dimension.

La sortie suivante est le tableau des GoF qui permettent d’évaluer la qualité d’ajustement du modèle :

On voit que le GoF absolu est de 0,465, très proche de son estimation bootstrap. Cette valeur est difficile à interpréter et sert surtout afin de comparer différents groupes d’individus ou différents modèles. Le Gof relatif et ceux basés sur les modèles internes et externes sont très élevés et auraient tendance à traduire une bonne qualité d’ajustement du modèle aux données.

Il faut ensuite vérifier les cross-loadings :

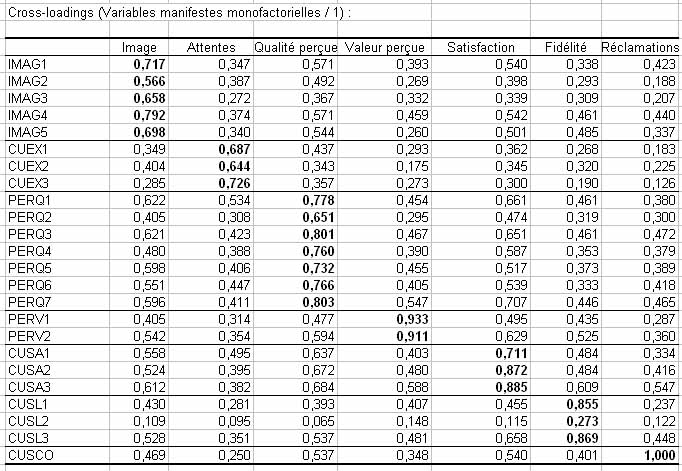
On vérifie que les loadings les plus élevés sont ceux reliant la variable manifeste à sa variable latente associée dans le modèle. C’est le cas ici. Deux tableaux détaillent les poids externes et les corrélations associées au modèle de mesure. Si on étudie le tableau des corrélations :

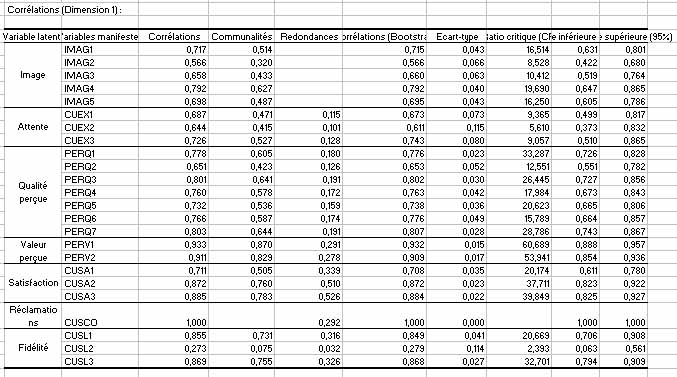
On peut voir que, par exemple, pour la variable satisfaction, CUSA3 et CUSA2 ont un plus fort impact sur la satisfaction que CUSA1. Ces tableaux permettent de connaître l’influence des variables manifestes sur les variables latentes.

Une fois le modèle de mesure étudié, le modèle structurel doit être analysé. Pour chaque variable latente, un certain nombre d’informations sont rassemblées. Nous prenons l’exemple de la satisfaction :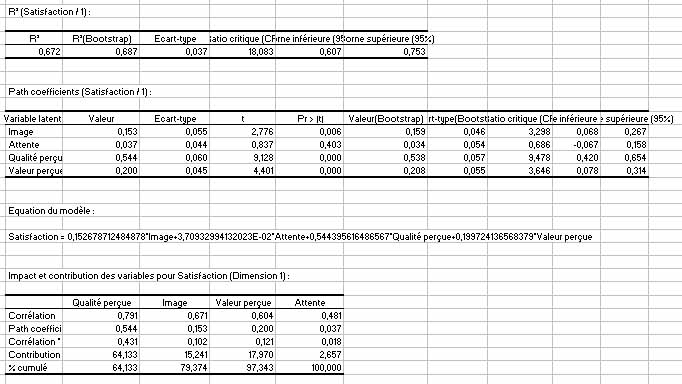

Ainsi, avec un R² de 0,672, on peut considérer que la variable latente est bien expliquée. On voit que c’est la qualité perçue qui a le plus fort impact sur la satisfaction suivie par la valeur perçue. L’impact des attentes est non significatif. Le dernier tableau résume l’ensemble des résultats précédents. On voit que la qualité perçue contribue à 64 % du R².

Le graphe suivant illustre les résultats précédents :

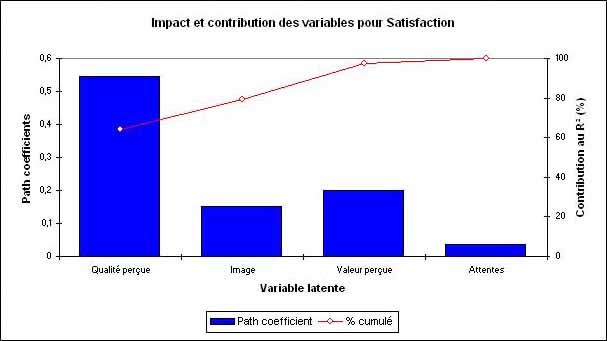
Par la suite, un tableau récapitule les indices de qualité prédictive principaux pour chacune des variables latentes. Ainsi, le R’² de la satisfaction est le plus élevé et les autres sont assez faibles. Les redondances sont toujours plus faibles que les communalités car l’approche PLS avec le mode A a tendance à favoriser le modèle de mesure.

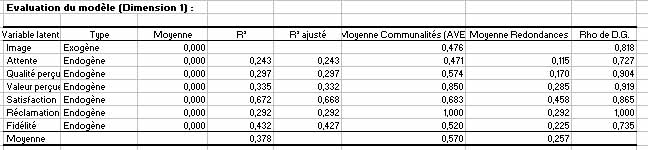
Dans la suite des sorties sont rassemblés les scores des variables latentes et les statistiques descriptives associées. Ces scores peuvent être réutilisés dans le cadre d’autres analyses statistiques avec XLSTAT.

Cette analyse nous a permis de présenter l’étude d’un jeu de données sur un modèle classiquement utilisé. Nous avons illustré l’utilisation de l’approche PLS qui permet de comprendre des interactions entre des concepts de manière claire. Une fois que le modèle est validé, il est simple d’interpréter les coefficients afin d’analyser les résultats.

Sorties sur le graphe :

Par ailleurs, XLSTAT-PLSPM permet de faire apparaître sur la feuille PLSPMGraph un grand nombre de paramètres. Pour se faire, il faut sélectionner ces paramètres. Appuyer sur le bouton suivant dans la barre d’outils

La boîte de dialogue « résultats » apparaît. Elle possède trois onglets : - le premier permet d’afficher un certains nombre d’indices sur les variables latentes dans le graphe :

- le second onglet permet d’afficher un certain nombre d’indices et de coefficients sur les flèches entre les variables latentes :

- le troisième onglet permet d’afficher un certain nombre d’indices et de coefficients sur les flèches entre les variables manifestes et la variable latente qui leur est associée :

Sélectionner les paramètres qui vous intéressent et cliquer sur OK. Toujours sur la barre d’outils, cliquer sur le bouton « afficher les résultats », ceux-ci apparaissent alors sur la feuille PLSPMGraph :