Modelo PLS básico: creación y ejecución

Este tutorial le mostrará cómo crear y ejecutar un proyecto básico de Modelo Path de Mínimos Cuadrados Parciales (Partial Least Squares Path Modeling, PLS-PM) en Excel usando el software XLSTAT.

Principios del modelado PLS

El modelado con mínimos cuadrados parciales (Partial Least Squares Path Modeling, PLS-PM) es una aproximación estadística al modelado de relaciones multivariables complejas (modelos de ecuaciones estructurales) entre variables observadas y latentes. Desde hace algunos años, esta aproximación ha gozado de una progresiva popularidad en varias ciencias (Esposito Vinzi et al., 2007). Los Modelos de Ecuaciones Estructurales incluyen distintas metodologías estadísticas que permiten la estimación de una red teórica causal de relaciones que vinvulan conceptos complejos latentes, cada uno medido por medio de un conjunto de indicadores observables. La primera presentación de una aproximación PLS finalizada a los modelos path con variables latentes fue publicada por Wold en 1979 y, en consecuencia, las principales referencias sobre el algoritmo PLS corresponden a Wold (1982 y 1985). Herman Wold opuso al “modelado duro” propuesto por LISREL (Jöreskog, 1970), que implicaba duras asunciones relativas a la distribución de los datos, y necesitaba varios cientos de casos) el “modelado blando” PLS (que tiene muy pocas asunciones respecto a la distribución, y que requiere de muy pocos casos). Estas dos aproximaciones a los Modelos de Ecuaciones Estructurales se han comparado en Jöreskog y Wold (1982). Desde el punto de vista de los modelos de ecuaciones estructurales, PLS-PM es un enfoque basado en componentes, donde el concepto de causalidad se formula en términos de esperanza condicional lineal. PLS-PM busca relaciones predictivos lineales óptimas en lugar de mecanismos causales, privilegiando así un proceso de descubrimiento orientado a la relevancia predictiva sobre la comprobación estadística de hipótesis causales. Dos artículos de revisión muy importantes en la aproximación PLS a los modelos de ecuaciones estructurales son Chin (1998, de orientación preferentemente aplicada) y Tenenhaus et al. (2005, más orientado a la teoría). Además, el modelado PLS se puede utilizar para el análisis de múltiples tablas y está directamente relacionado con los métodos de análisis de datos más clásicos utilizados en este campo. De hecho, PLS-PM puede considerarse también como un enfoque muy flexible para realizar análisis multi-bloque (o tabla múltiple) mediante el modelo PLS jerárquico y el modelo PLS de confirmación (Tenenhaus y Hanafi, 2007). Este enfoque muestra claramente cómo la tradición del análisis de tablas múltiples “orientada a los datos” en alguna medida puede fusionarse con la tradición “orientada a la teoría” de los modelos de ecuaciones estructurales, de suerte que permite llevar a cabo análisis de datos multi-bloque a la luz del conocimiento actual sobre las relaciones entre las tablas. En este tutorial le guiaremos paso a paso para mostrarle cómo crear un proyecto, definir un modelo, estimar los parámetros y analizar los resultados. Este tutorial se basa en el siguiente documento: [Tenenhaus M., Esposito Vinzi V., Chatelin Y.-M. and Lauro C. (2005). PLS Path Modeling. Computational Statistics & Data Analysis, 48(1), 159-205].

Modelos path PLS con XLSTAT-PLSPM

Datos para el análisis de modelos path PLS

La aplicación se basa en datos reales. Se encuestó a total de 250 clientes de teléfonos móviles y se les hicieron varias preguntas para modelar su lealtad a la marca. El modelo PLSPM se basa en el Índice Europeo de Satisfacción del Consumidor (European Customer Satisfaction Index, ECSI). En el modelo ECSI, las variables latentes (conceptos que no pueden medirse directamente) se interrelacionan como aparece en el siguiente diagrama.

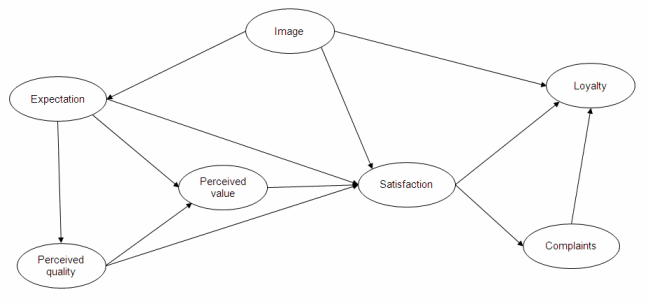
Cada variable latente se refiere a una o más variables manifiestas (estas variables son las que se miden directamente). En este ejemplo, las preguntas (variables manifiestas) se evalúan en una escala de 0 a 100. Por ejemplo, la variable latente Imagen es medida con estas 5 variables manifiestas:

• Se puede confiar en lo que dice y hace
• Es estable, y está firmemente establecida
• Hace una contribución a la sociedad
• Se preocupa por los clientes
• Es innovadora y tiene visión de futuro

Puede descargar una hoja XLSTAT-PLSPM con los datos y resultados para usar en este tutorial haciendo clic aquí. Los proyectos XLSTAT-PLSPM son plantillas especiales de libro de trabajo de Excel. Cuando creamos un nuevo proyecto, su nombre por defecto comienza por PLSPMBook. Puede luego guardarlo con el nombre que desee, pero asegúrese de usar los comandos “Guardar” o “Guardar como” del menú XLSTAT-PLSPM para guardarlo en una careta dedicada a los proyectos PLSPM usando la extensión *.ppmx.

Nota: cuando abra el archivo PLSPathModeling_ECSI.ppm, la representación gráfica podría quedar mal. Esto se debe al hecho de que la representación depende de la configuración de pantalla. Para mejorar la visualización, haga clic en el botón “Optimizar la pantalla” (véase más adelante). Un proyecto XLSTAT-PLSPM en bruto contiene dos hojas que no pueden eliminarse:

• D1: Esta hoja está vacía y hay que añadir todos los datos de entrada que desea utilizar en esa hoja de cálculo.
• PLSPMGraph: Esta hoja está en blanco y se utiliza para diseñar el modelo. Al seleccionar esta hoja, el menú “Modelo Path” aparece en la parte superior izquierda de la página.

Configuración de un modelo path PLS

Para crear el proyecto usado en este tutorial, generamos en primer lugar un nuevo proyecto usando el menú XLSTAT-PLSPM:

El modelado path PLS es un método complejo y el módulo PLSPM de XLSTAT tiene muchas opciones y características específicas. Con el fin de simplificar la aplicación de un modelo sencillo, dos pantallas están disponibles.

La opción por defecto, denominada “clásica”, muestra las principales funciones necesarias para aplicar el modelo path PLS. Otra más sofisticada, denominada “experta”, muestra una gran cantidad de nuevas opciones como las pruebas multigrupo, moderación de la estimación del efecto, el procedimiento Superbloc... Para modificar esta opción , haga clic en el botón de opciones XLSTAT-PLPM en la barra de herramientas XLSTAT-PLSPM.

Entonces lo guardamos como PLSPM_ECSI.ppmx usando el comando Guardar como del mismo menú.

A continuación, copiamos los datos que teníamos disponibles en un archivo de Excel, y les pegamos en la hoja D1 del Proyecto. Una vez hecho esto, estamos listos para empezar a crear el modelo. Vamos a la hoja PLSPMGraph. La barra de herramientas aparece en la esquina superior izquierda de la hoja. Puede encontrar información sobre la función de cada botón en la ayuda.

Para crear varias variables latentes en una fila, haga doble clic en el botón círculo para que quede presionado mientras añade variables:

A continuación, puede agregar las flechas que indican cómo se relacionan las variables latentes. Para añadir una flecha, haga clic en la variable latente de la que debe partir y, a continuación, pulse Ctrl y haga clic en la variable latente en la que la flecha debe terminar. A continuación, haga clic en el botón de flecha o utilice la siguiente combinación de teclas: Ctrl + L.

Una vez que se han añadido todas las flechas, se pueden definir las variables manifiestas que se relacionan con cada variable latente (esto también se puede hacer después de la adición de las variables latentes). Para añadir variables manifiestas a una variable latente, seleccione la variable latente y haga clic en el botón MV en la barra de herramientas:

Esto activa la hoja de D1 y muestra un cuadro de diálogo en el que dar un nombre propio a la variable latente, seleccionar las variables manifiestas en D1 y definir algunas opciones de configuración.

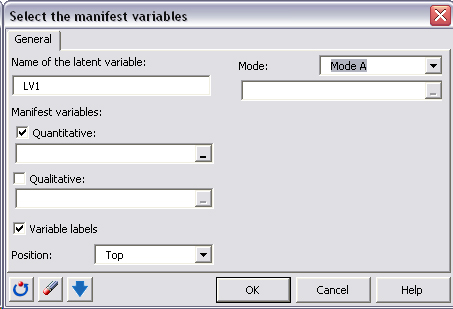
Es preciso definir el modo (reflectivo o formativo). En el Modo A (modo reflectivo) la variable latente es responsable de lo que se mide mediante las variables manifiestas, y en el modo B (modo formativo), las variables manifiestas construyen o “forman” la variable latente. Por ejemplo, esta es la forma en que aparece el cuadro de diálogo una vez rellenado para la variable latente Expectativas:

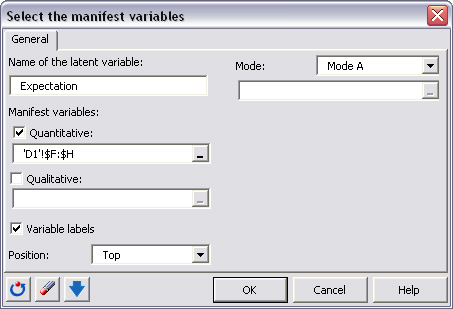
El modelo obtenido tiene la siguiente forma:

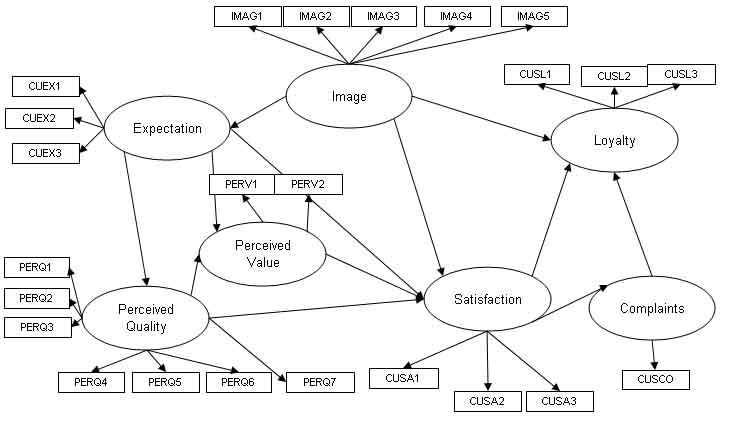
Una vez que se han definido las variables manifiestas para cada variable latente y las variables latentes están vinculadas, puede comenzar a calcular el modelo. Para ejecutar el modelo, haga clic en el botón de reproducción.

Esto muestra el cuadro de diálogo Ejecutar, y en él disponemos de muchas opciones. Para este tutorial se han utilizado las siguientes opciones:

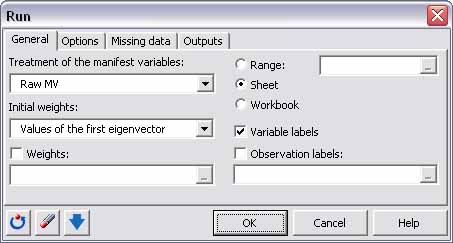
El modelo path PLS se basa en un algoritmo iterativo y por lo tanto debe ser inicializado. Para esta aplicación, las variables manifiestas (i.e., variables observadas) son tratadas sin transformaciones previas (están disponibles 4 ajustes diferentes) porque todas las variables están en la misma escala. Los valores iniciales de los pesos exteriores (“outer weights”) son los valores del primer vector propio cuando se realiza un análisis de componentes principales sobre las variables manifiestas asociadas a una variable latente (disponemos de 2 ajustes diferentes).

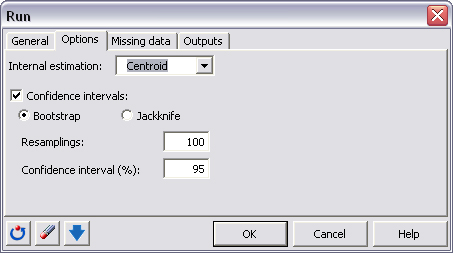
Utilizamos el sistema centroide para la estimación de los pesos internos (“inner weights”). Los intervalos de confianza se obtienen utilizando remuestreo bootstrap.

En nuestro ejemplo simple, no tenemod datos perdidos. Seleccionamos por tanto No aceptar datos perdidos.

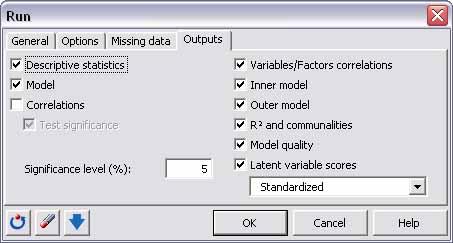
Por último, en los resultados, todas las casillas están marcadas (excepto correlaciones). Vamos a estudiar cada salida en el siguiente apartado.

Resultados e interpretación de un proyecto PLS-PM

En los resultados, se resume en primer lugar información referida a las variables manifiestas, el modelo de medida y el modelo estructural.

Resultados numéridos del análisis de un modelo path PLS

Los primeros elementos importantes son los índices de fiabilidad compuesta:

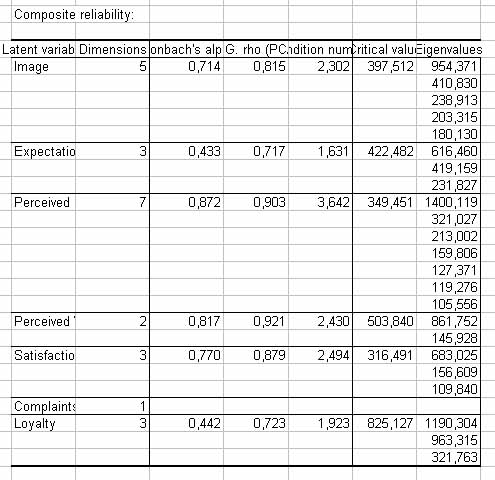
En esta aplicación, las variables latentes son reflectivas. Los bloques tienen que ser unidimensionales. Podemos ver que la rho de Dillon-Goldstein es mayor que 0.7 y que el primer valor propio es siempre mucho mayor que el segundo. Las variables Expectativas y Lealtad tienen valores malos en el alfa de Cronbach y una segunda dimensión podría ser significativa. En este tutorial, nos centraremos en el caso de una dimensión. Si usted está interesado en otras dimensiones, puede estudiar las correlaciones entre las variables manifiestas y los factores en un análisis de componentes principales aplicado en cada bloque de variables manifiestas. No nos centraremos ahora en este asunto, y consideraremos solo una dimensión. La aplicación modelo path PLS da la tabla con los índices GoF:

Podemos ver el GoF absoluto es 0.465, muy cerca de la estimación bootstrap. Este valor es difícil de interpretar; podría ser útil para comparar la calidad global de dos grupos de observaciones o dos modelos diferentes. El GoF relativo es muy alto. También lo son los índices GoF de los modelos interno (“inner model”) y externo (“outer model”). Seguidamente, debemos comprobar las cargas o saturaciones cruzadas:

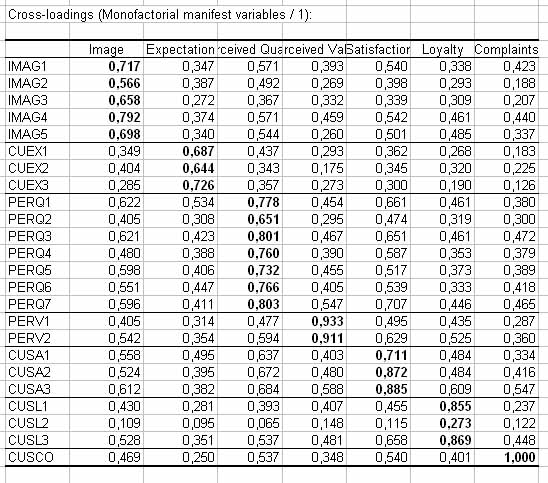
En el caso de nuestros datos, vemos que las saturaciones entre las variables manifiestas o indicadores y su propia variable latente son las más altas (en negrita) comparadas con las saturaciones de cada indicador con el resto de las variables latentes (en tipografía normal). Seguidamente se agrupan los pesos exteriores (“outer weights”) y las correlaciones en dos grandes tablas. Si estudiamos las correlaciones entre las variables manifiestas y variables latentes tenemos lo siguiente:

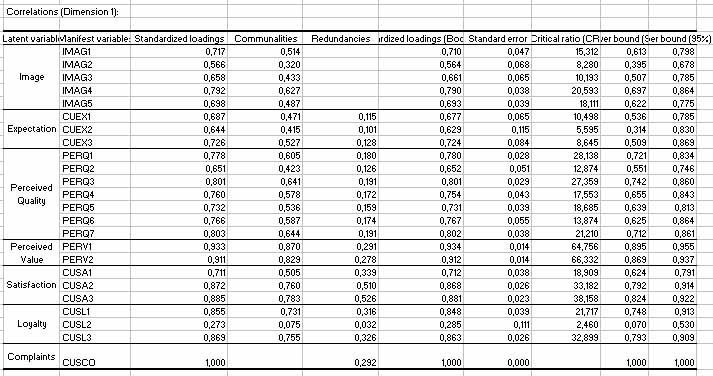
Podemos ver que, por ejemplo, las variables manifiestas CUSA3 y CUSA2 tienen un mayor efecto sobre la satisfacción que CUSA1. Estas tablas permiten ver el impacto de cada una de las variables manifiestas en su variable latente asociada. Se presentan a continuación los resultados asociados con el modelo estructural. Para cada variable latente, se recoge información sobre el modelo estructural. En el caso de la satisfacción, tenemos:

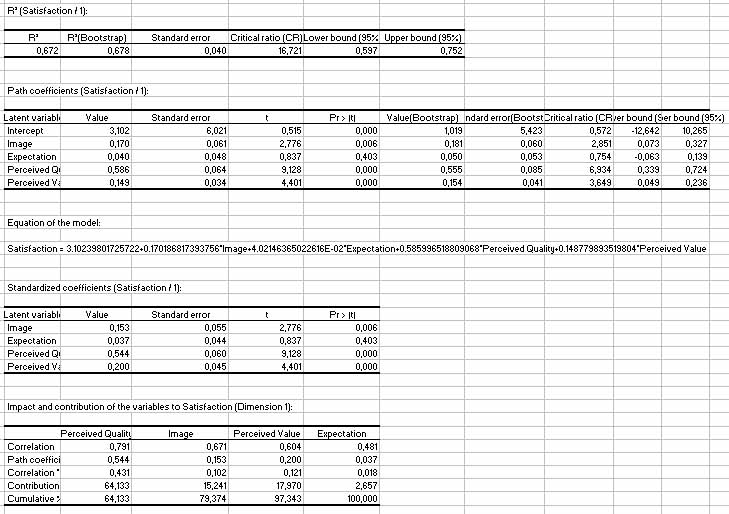
Un coeficiente R2 de 0.672 puede considerarse como un buen resultado. Podemos ver que la calidad percibida tiene el mayor efecto sobre la satisfacción (.586), y que el impacto de las expectativas (.040) no es significativo. En la última tabla se resumen los resultados. Podemos ver que el valor percibido contribuye al 64% del coeficiente R2 de satisfacción. El gráfico proporciona una representación gráfica de estos resultados:

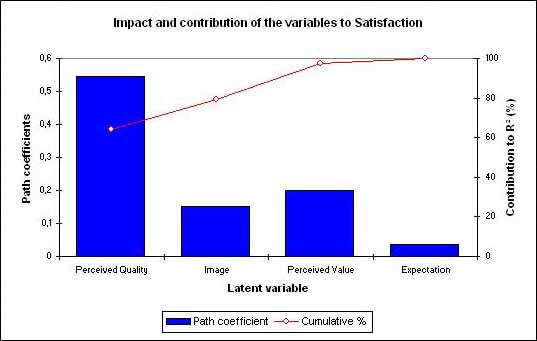
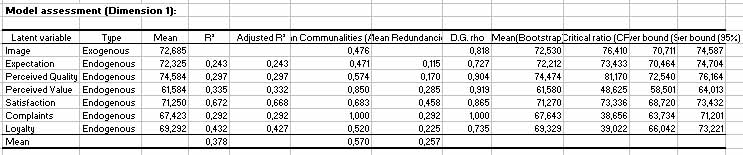
La siguiente tabla muestra los diferentes índices de calidad de predicción asociados tanto al modelos externo como al interno para cada variable latente. Los valores medios de estos índices proporcionan un valor de calidad global. Vemos que la media de todos estos coeficientes es 0.378, y que el coeficiente R2 de satisfacción es el más alto (0.672). Las comunalidades son siempre mayores que las redundancias porque PLSPM favorece el modelo de medición en su procedimiento de estimación.

Una de las mayores ventajas de PLSPM es que proporciona puntuaciones (“scores”) de las variables latentes, puntuaciones se pueden utilizar en otros tratamientos estadísticos con XLSTAT. Este estudio ha demostrado cómo utilizar el módulo XLSTAT-PLSPM en el caso de datos reales. Una vez que el modelo ha sido elaborado, el procedimiento es sencillo. Tras la validación del modelo, la interpretación de los resultados se puede hacer mediante la lectura de las tablas con coeficientes path y correlaciones.

Salida gráfica del análisis de modelos path PLS

Podemos mostrar muchos tipos de resultados en el modelo path con XLSTAT-PLSPM. Elija entre todos los índices posibles obtenidos al hacer clic en el botón “Elegir resultados a mostrar”.

Aparece el cuadro de diálogo de Resultados. Tiene tres páginas: la primera tiene que ver con mostrar los índices en las variables latentes; la segunda, con mostrar los coeficientes y los índices de las flechas entre las variables latentes, y la tercera con mostrar los coeficientes e índices de las flechas entre las variables manifiestas y las latentes. Los resultados aparecen en el modelo path en la hoja PLSPMgraph cuando pulsamos el botón “Mostrar resultados”.

Puede seleccionar todo el diagrama y copiarlo en otro documento.