Tamaño muestra y potencia regresión múltiple

Este tutorial muestra cómo calcular el tamaño de una muestra y la potencia estadística para una regresión múltiple en Excel usando el software estadístico XLSTAT. Â

XLSTAT-Modelado de datos ofrece una herramienta a aplicar a un modelo de regresión lineal. XLSTAT estima la potencia o calcula el número necesario de observaciones asociado con variaciones de R2 en el marco de una regresión lineal. Cuando sometemos a prueba una hipótesis usando una prueba estadística, hemos de tomar algunas decisiones: - La hipótesis nula H0 y la hipótesis alternativa Ha.

• La prueba estadística a utilizar.
• El error tipo I, también conocido como alfa. Ocurre cuando rechazamos la hipótesis nula siendo verdadera. Se fija a priori para cada prueba y es el 5%.

El error tipo II o beta es menos estudiado, pero tiene gran importancia. De hecho, representa la probabilidad de que no rechacemos la hipótesis nula cuando es falsa. No podemos fijarla de antemano, sino que, basándonos en otros parámetros del modelo, podemos tratar de minimizarlo. La potencia de una prueba se calcula como 1-beta, y representa la probabilidad de rechazar la hipótesis nula cuando es falsa. En consecuencia, queremos maximizar la potencia de la prueba. XLSTAT calcula la potencia (y beta) cuando otros parámetros son conocidos. Para una potencia determinada, permite también calcular el tamaño de muestra necesario para alcanzar dicha potencia. Los cálculos de la potencia estadística se hacen habitualmente antes de llevar a cabo el experimento. La principal aplicación de los cálculos de la potencia es estimar el número de observaciones necesarias para llevar a cabo adecuadamente un experimento. En un próximo estudio, deseamos analizar los pesos de los niños de acuerdo al tamaño y la edad (como sucede en el siguiente tutorial sobre Regresión Lineal Múltiple). Deseamos saber el el valor R2 de este modelo es significativamente diferente de 0. Hay dos variables independientes o predictores, y nos gustaría saber cuántos niños deberían ser evaluados para obtener una potencia de 0.9. Puesto que no conocemos aún los parámetros de nuestras muestras, utilizaremos el concepto de tamaño del efecto. Cohen (1988) introdujo este concepto, que proporciona un orden de la magnitud para el tamaño del efecto, es decir, la diferencia relativa entre las medias. Así, someteremos a prueba tres tamaños del efecto: 0.02 (efecto pequeño), 0.15 (efecto moderado) y 0.35 (efecto grande). Puesto que el tamaño del efecto se basa en la diferencia entre las medias, se espera que para un mayor efecto, el tamaño de muestra requerido sea más pequeño.

Datos para calcular el tamaño de la muestra o la potencia estadística en una regresión múltiple

Puede descargar una hoja Excel con los datos y resultados utilizados en este tutorial haciendo clic aquí.

Configuración del cálculo del tamaño de la muestra o la potencia estadística en una regresión múltiple

Tras abrir XLSTAT, hacemos clic en Análisis de potencia y elegimos Regresión lineal.

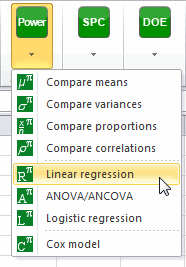
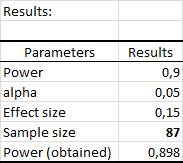
Una vez hacemos clic en el botón, aparece el cuadro de diálogo. Debemos elegir el objetivo Encontrar el tamaño de la muestra. Seleccionamos luego la prueba R2 diferente de 0. El nivel de alfa es 0.05. La potencia deseada es 0.9. El número de predictores o variables explicativas es 2. En lugar de seleccionar parámetros de entrada detallados, seleccionamos la opción Tamaño del efecto y escribimos el valor de 0.02 (efecto débil).

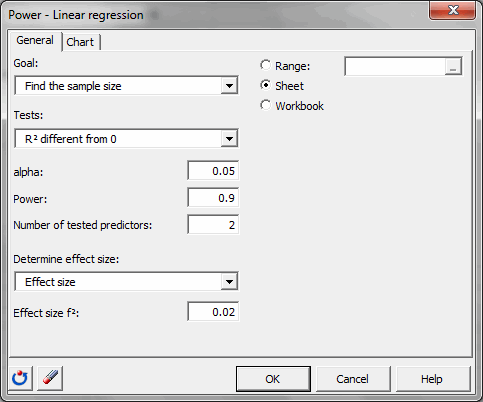
En la pestaña Gráficos, la opción Gráfico de las simulaciones; el “tamaño de la muestra 1” se mostrará en el eje vertical, y la “Potencia” en el eje horizontal.

La potencia varía entre 0.8 y 0.95 en incrementos de 0.01.

Tras hacer clic en el botón OK, comienzan los cálculos, y luego se muestran los resultados.

Resultados del cálculo del tamaño de la muestra o la potencia estadística en una regresión múltiple

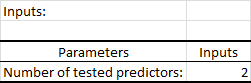
La primera tabla muestra los parámetros usados como entrada. En nuestro caso, aparece solo el número de predictores.

The second table shows the calculation results and an interpretation of the results.

Vemos que necesitamos 636 observaciones para obtener una potencia lo más próxima posible a 0.9.

La siguiente tabla resume los cálculos obtenidos para cada valor de la potencia entre 0.8 y 0.95.

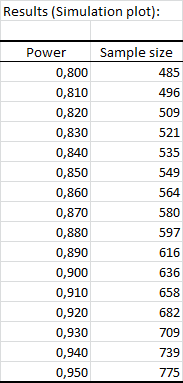
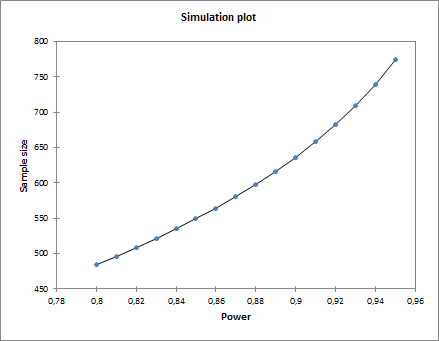
El gráfico de simulación muestra la evolución del tamaño de la muestra dependiendo de la potencia. Vemos que para una potencia de 0.8, necesitamos algo más de 485 observaciones por muestra y, conforme la potencia llega a 0.95, llegamos a 775 observaciones.

For effect sizes of 0.15 and 0.35, we obtain the following results:

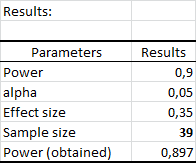
Por tanto, el tamaño de la muestra cae conforme R2 se aparta de 0, y vemos que, para una diferencia grande, serían suficientes 39 observaciones.

De este modo, si asumimos que la calidad de la explicación de las variables edad y peso sobre el peso de un niño es fuerte (R2 próximo a 1), 39 observaciones serán suficientes para obtener una potencia de 0.9.

XLSTAT es una potente herramienta tanto para investigar el tamaño muestral requerido para un análisis, como para calcular la potencia de una prueba. Obviamente, si el usuario tiene más información acerca de las muestras o las poblaciones, puede dar detalles de los parámetros de entrada, en lugar de limitarse a usar el tamaño del efecto.