Excelでの主成分分析 (PCA)

このチュートリアルは、XLSTATソフトウェアを用いてExcel内で主成分分析 (PCA: Principal Component Analysis) をセットアップして解釈することを支援します。

これがあなたの必要とする正しい多変量データ解析ツールであるかどうか不確かな場合は、こちらのガイド を参照してください。

Excelで主成分分析を実行するデータセット

データと結果のExcelシートは、下のボタンをクリックしてダウンロードできます : データをダウンロード

このデータ は、 米国国勢調査局からのもので、2000年と2001年の間の51州の人口の変化を記述しています。元のデータ集合は、分析の焦点である2001年のデータとの1000人の住民ごとの比率に変形されています。このデータセットは、階層クラスタリング チュートリアルもの使用されています。

このチュートリアルの目的

我々の目的は、変数間の相関を分析して、いくつかの州で他の州よりもとても異なる人口の変化があるかどうかを発見することです。

主成分分析とは何か

主成分分析は、M個のオブザベーション / N個 の変数 の表にまとめられた数値データを分析するのにとても便利な手法です。それは次のようなことができます:

• N個の変数間の相関を素早く可視化し分析する。
• M個のオブザベーション（もともとはN個の変数で記述される）を低次元のマップ、変動基準の最適な表示で、可視化し分析する。
• P個の非相関係数の集合を構築する。

主成分分析の限界は、それが射影手法であることに由来します。そして、ときどきその可視化は間違った解釈を導きます。ただし、これらの落とし穴を避けるためにいくつかの方法があります。

またPCAは探索的統計ツールであり、一般的に仮説を検定することができないことに注意することも重要です。この側面の利点は、解釈のために正当な限り、オブザベーションまたは変数を除去したり追加したりして、 PCAが複数回実行されることです。

XLSTATを用いたExcelでの主成分分析のセットアップ

データの選択

XLSTATを起動して、XLSTAT / データ解析 / 主成分分析 コマンド（下図）を選択してください。

主成分分析ダイアログ・ボックスが現れます。

Excelシートでデータを選択してください。

この事例では、データは最初の行から始まっていますので、列選択を使うのが速くて簡単です。これは、列に対応する文字が選択ボックスの中に表示される理由を説明します。

選ばれたデータ形式は、入力データの形式により、オブザベーション/変数です。

主成分分析: 選択するタイプ - Pearson または共分散

計算の際に使用するPCAタイプは、伝統的な相関係数に対応するPearsonの相関行列です。共分散行列は、分散が大きい変数により多くの重みを割り当てます。

XLSTATでの主成分分析、出力とチャートの設定

出力タブでは、有意な相関を太字で表示するオプション（有意度の検定）を有効にするように選びます。

チャートタブでは、すべてのチャートにラベルを表示し、すべてのオブザベーションを表示（オブザベーション・チャートとバイプロット）するために、フィルタ・オプションのチェックをはずします。たくさんのデータがある場合は、ラベルの表示は、結果の全体表示を遅くするかもしれません。すべてのオブザベーションの表示は、結果を読みにくくするかもしれません。その場合、表示するオブザベーションのフィルタリングを推奨します。

XLSTATでの主成分分析 - 計算の開始

OKをクリックすると計算が始まります。行数と列数を確認するように促されます。

注意: このメッセージは、XLSTAT オプション・パネルで、”選択確認の要求”を非選択にして回避できます。

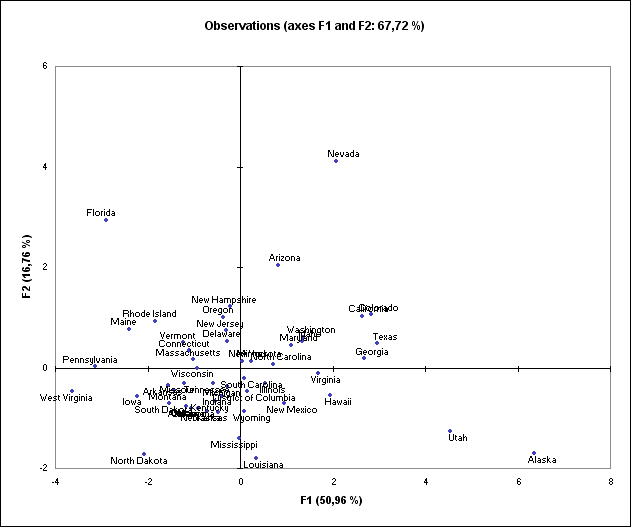
そして、プロットを表示したい軸を確認します。この事例では、最初の2軸で説明される変動のパーセンテージが、67.72%ととても高いです。結果の誤解釈を避けるために、我々は、軸1と軸3上の2番目のチャートによって結果を補完することにします。

XLSTATを用いたExcelでの主成分分析の結果の解釈

PCA 相関行列の解釈の仕方

注目するべき最初の結果は、相関行列です。65歳より上と下の人々の比率が負に相関している(r = -1)ことがわかります。結果の品質への影響なしに、2つの変数のどちらかを除去することができたでしょう。 また、Net Domestic Migration は、Net International migrationを含む他の変数と低い相関を持つこともわかります。これは、米国民および非米国民がさまざまな理由で州を移動しているであろうこを意味しています。

主成分分析での固有値の解釈の仕方

次の表と対応するチャートは、N次元の元の表（この事例ではN=7）からより低い次元への写像の品質を反映する固有値という数学的なオブジェクトに関係しています。この事例では、1番目の固有値は、3.567 に等しく、変動の合計の51%を説明していることがわかります。 これは、もし我々がそのたった1つの軸上でデータを説明した場合、データの変動の合計の何パーセントをまだ見ることができるかを意味します。 各固有値は因子に対応しており、各因子は1つの次元に対応しています。因子は、元の変数の線形結合になっており、すべての因子は非相関(r=0) です。固有値と対応する因子は、それらが元の分散をどれだけ説明するか（%に変換）により降順に並び替えられています。

大まかに言えば、因子 = PCA 次元 = PCA 軸 です。

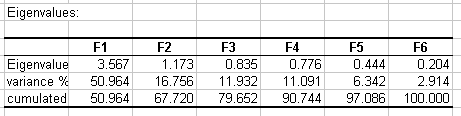
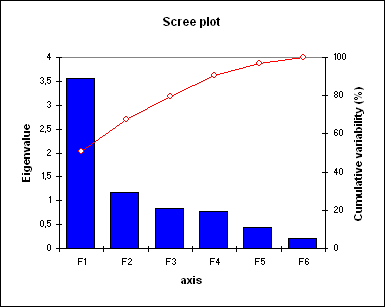
理想的には、最初の2つか3つの固有値が高い分散に対応し、最初の2つか3つの因子に基づくマップが、元の多次元の表の品質のよい写像であることを 保証するでしょう。この事例では、最初の2つの因子で、データの元の分散の 67.72%を説明することができます。 これは良い結果ですが、いくらかの情報が次の因子に隠れているかも知れないので、マップを解釈するときには注意深くなければなりません。もとは7つの変数 を持っていましたが、因子の数は6だということがわかります。 これは、負の相関(-1)を持つ2つの年齢の変数のためです。"役に立つ"次元の数が、自動的に探索されます。

PCAでの変数に関係する結果の解釈の仕方

1番目のマップは、相関円（correlation circle）と呼ばれます（下図のF1とF2軸上）。それらは因子空間での元の変数の写像です。2つの変数が中央から遠くて、もしそれらが： お互いに接近していたら、それらは有意に正の相関である (r が1に近い)、 もしそれらが直交していたら、それらは相関していない (rが0に近い)、 もしそれらが中央をはさんで反対側にあれば、それらは有意に負の相関である(rが-1に近い) 、と解釈できます。 変数が中央に近い場合、それはいくらかの情報が他の軸に乗っていて、どのような解釈も危険であることを意味します。たとえば、変数 Net Domestic migration とNet International Migrationの間の相関を解釈するように誘惑されるかも知れませんが、実際には、相関はありません。これは相関行列を見るか、F1と F3軸上の相関円で見て確認することができます。

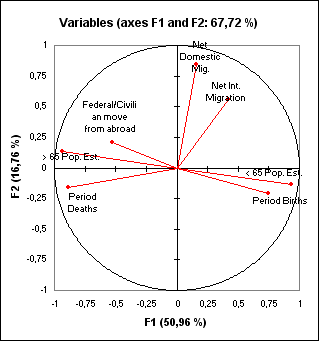
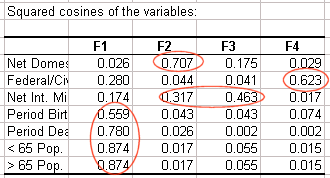
相関円は軸の意味を解釈するのに役立ちます。この事例では、水平の軸は年齢 と人口の更新、垂直の軸は国内移住にリンクしています。これらの傾向は、次のマップを解釈するのに役立ちます。変数が軸によくリンクしていることを確かめるために、cos2乗の表をご覧ください： cos2乗がより大きいほど対応する軸へのリンクがより大きいことを意味します。任意の変数のcos2乗がよりゼロに近いほど、対応する軸上のトレンドの観点から結果を解釈するときはより慎重でなければなりません。 この表を見て、我々は、国際移住のトレンドはF2/F3軸上で最もよく見えることがわかります。

PCAでのオブザベーションに関係する結果の解釈の仕方

次のチャートは、主成分分析（PCA）の究極の目的かもしれません。それは2次元のマップでデータを見て、トレンドを識別することを可能にします。ネバダ州とフロ リダ州の人口統計はユニークで、ユタ州とアラスカ州の人口統計がそうであるように、共通の特徴を持っている2つの州だとわかります。表に帰って、ユタ州 とアラスカ州が65歳を超える人々の人口比率が低いことを確認できます。ユタ州は米国で最高の出生率で、アラスカ州も高くランクされています。

バイプロットを表示することもできて、それはPCA空間での変数とオブザベーションの同時表現です。

XLSTAT-3DPlotで生成された最初の3つの軸上の3D可視化を見るにはクリックしてください。

主成分分析の活用上の注意

主成分分析は、回帰分析の前に相関する変数を使用することを避けるために、またはデータのクラスタリングの前に変数のより良い概観を得るために、しばしば実行されます。クラスタの数が、マップ上で簡単に推測できることがよくあります。上の人口動態データは、階層クラスタリングのチュートリアルでも使用されました。 ">65 pop" 変数は、年齢変数の重みが2倍になるので、分析から除去されました。

さらに: PCAに追加変数の追加

計算の後、PCAに追加変数（補助変数）を追加することが可能です。これは解釈の品質を向上させることを助けるでしょう。XLSTATでは、それらの変数は、PCAダイアログ・ボックスの追加データタブで選択できます。追加変数を2つのタイプに分かれます:

- 質的追加変数: それらが属するカテゴリに応じてマップ上のオブザベーションを色付けできます。このチュートリアルの事例では、ある州の大部分が共和党員であるか、大部分が民主党員であるかを定義する列を加えることができました。

- 量的追加変数: これらの変数は、それらがPCAを構築するのに使用した変数のグループとどのように相関するかを見るために追加できます。PCAが回帰の前に実行される場合、説明変数はPCAを構築するために使用できますが、一方、従属変数は追加変数として追加できます。これは、どの説明変数が従属変数に対して強い効果を持つかを大まかに検出するのを助けるでしょう。

以下の動画は、 PCA と XLSTATでのその実装をよりよく理解することを助けます。