平均の比較検定での必要な標本サイズまたは検出力

XLSTAT-Parametric testsは、t検定とz検定という平均を比較する複数の検定を含みます。XLSTAT-Powerは、これらの検定の検出力を評価し、十分な検出力を得るため必要なオブザベーションの数を計算することを可能にします。

統計的検定を用いて仮説を検定するとき、なすべき複数の決定があります：

• 帰無仮説 H0 と対立仮説 Ha。
• 使用する統計的検定。
• アルファとしても知られる第1種の過誤。これは、帰無仮説が真であるときに、それを棄却するときに起きる。これは、各検定で事前に設定され、5%である。

第2種の過誤またはベータは、あまり調査されていませんが、とても重要です。実際、それは帰無仮説が偽であるときに、それを採用する確率を表します。我々は前もってこれを固定することはできませんが、モデルの他のパラメータに基づいて、それを最小化することができます。検定の検出力は、1-ベータ として計算され、帰無仮説が偽であるときに、それを棄却する確率を表します。

したがって、我々は、検定の検出力を最大化したいのです。XLSTAT-Powerモジュールは、他のパラメータが既知であるときに、検出力（およびベータ）を計算します。ある検出力ついて、その検出力に達するために必要な標本サイズを計算することもできます。統計的検出力の計算は、通常、実験が実施する前に行われます。検出力の計算の主な応用は、実験を適切に行うために必要なオブザベーションの数を推定することです。

2つの独立した標本の比較を行います。帰無仮説H0: 平均1 – 平均2 = 0、に基づくt検定で、0.9の検出力を得るために必要なオブザベーションの数を知りたいとします。我々は標本のパラメータをまだ知らないので、効果量のコンセプトを用います。 Cohen (1988) は、効果量の大きさを提供するコンセプト、すなわち、平均間の相対差を導入しました。そして、我々は3つの効果量を検定します：小さな効果の0.2、中ぐらいの効果の0.5、そして強い効果の0.8。効果量は平均間の差に基づくので、効果が大きいほど、要求される標本サイズが小さくなることが期待されます。

平均の比較検定の検出力を計算するためのデータセット

この事例の結果を格納しているExcel スプレッド・シートは、こちらをクリックしてダウンロードできます。

平均の比較検定の検出力のセットアップ

XLSTATを開くと、Power アイコンをクリックして、平均を比較を選びます。

ボタンをクリックすると、ダイアログ・ボックスが現れます。 目標 標本サイズを見つけるを選び、独立の2標本についてのt 検定を選び、対立仮説として "平均1 <> 平均2を取ります。アルファは0.05です。要求される検出力は0.9です。我々は、我々の標本のサイズが等しいと仮定するので、N1/N2 比は1に等しいです。詳細な入力パラメータの代わりに、我々は、効果量オプションを選択して、弱い効果の0.2を入力します。

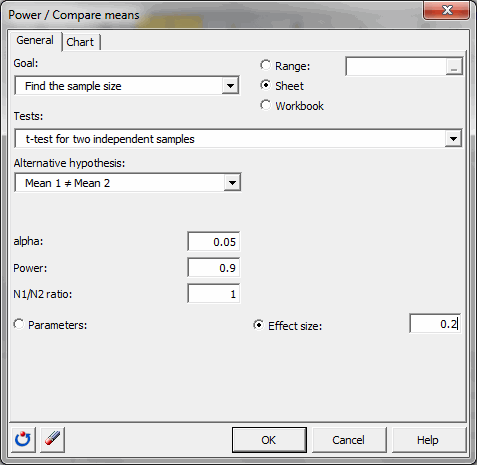
チャート・タブでは、"シミュレーション・プロット” を有効にして、垂直軸に標本1のサイズを表示し、水平軸に検出力を表示するように選びます。検出力は、0.8から0.95 の範囲で、増分を 0.01とします。

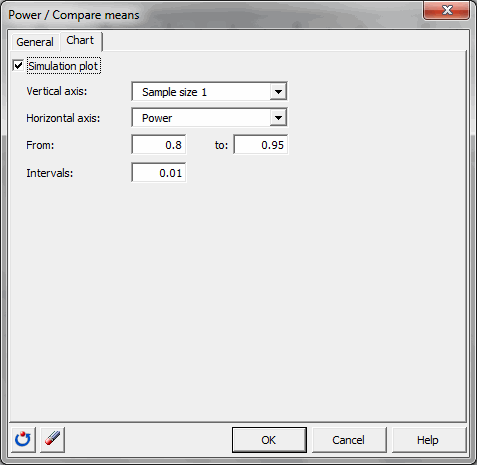
OKボタンをクリックすると、計算が行われ、結果が表示されます。

平均の比較検定の検出力の計算の結果

最初の表は、計算結果と結果の解釈を示します。

できる限り0.9に近い出力を得るには、標本ごとに526 個のオブザベーションを必要とすることがわかります。

下記の表は、0.8 から 0.95の間の検出力の各値で得られた計算を要約します。

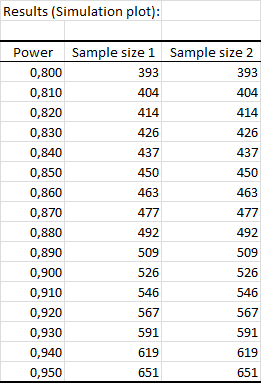
シミュレーション・プロットは、検出力に基づく標本サイズの計算を示します。0.8の検出力では、標本ごとに393 個強のオブザベーション、0.95 の検出力では651 個のオブザベーションを取ります。

0.5 と0.8の効果量では、我々は以下の結果を得ます：

したがって、平均間の差が増大するので、大きな差では、標本サイズは落ちて、 標本ごとに34 個のオブザベーションで十分になります。

XLSTAT-Power は、分析に必要な標本サイズを調査することと、検定の検出力を計算することの両方でパワフルなツールです。 明らかに、ユーザーが標本または母集団に関するより詳細な情報を持つ場合、効果量を用いるよりも、入力パラメータの詳細を与えることもできます。

お問合わせは、マインドウエア総研へ。