ExcelでのBreusch-Pagan & White分散不均一性検定チュートリアル

XLSTATで分散不均一性検定を実行するデータセット

このチュートリアルでは、均一分散のモデルと強い不均一分散のモデルを比較する目的で作成した人工データを使用します。このデータは、糖度と新品種のフルーツのサイズにおける年齢（age:日数で計測）の効果をテストする目的の実験です。

データ、結果および追加の情報のExcelシートは、 こちらをクリックしてダウンロードできます。

"age "を説明変数とみなして2つの単純な 線形回帰 が実行されました。 我々は、1番目と2番目の回帰でそれぞれ糖度（sugar content）とサイズ（size）を従属変数として使用します。データセットにおける2つの回帰の残差が表示されます。

1番目の回帰 (sugar content)が均一分散を示すのに対して、2番目(size) は強い不均一分散です。

データを収集する技術的な方法は、このチュートリアルの最後に説明しています。.

このチュートリアルの目的

このチュートリアルの目的は、線形回帰における従属変数（たとえば、sugar content または size）の変動が説明変数（age）によって変化するかどうかを確認することです。技術的には、我々は、回帰残差が説明変数に対して均一に分散するかどうかを問います。その場合、我々は不均一分散について語ります。生物のサイズは年齢によって、よりまちまちになることがとてもよくあります。赤ちゃんから大人 までを比較すると、赤ちゃんは相対的に“標準”の身長であるのに対して、大人の身長はより変動します。これは、不均一分散の典型例です。

我々は、2つの極端な状況（均一分散と強い不均一分散）で、これらの検定をどのように実行するかを示すために、Breusch-Pagan and White 不均一分散検定を使用します。

不均一分散検定: どのような仮説を検定するのか?

不均一分散検定は、以下の2つの仮説を示唆します。

H0 (帰無仮説): データは均一分散である。

Ha (対立仮説): データは不均一分散である。

したがって、不均一分散検定に関するp値が、ある一定のしきい値（たとえば0.05 ）より低い場合、そのデータは有意に不均一分散であると結論づけられます。

XLSTATにおける不均一分散検定の実行

XLSTATメニューを開いて、 Time / 不均一分散の検定をクリックします。残差ボックスで、残差(Sugar) の列を選び、説明変数ボックスでAgeの列を選びます。White 検定のチェックボックスをチェックして、OK ボタンをクイックして分析を起動します。この最初の分析の結果が新しいシートに表示されます。

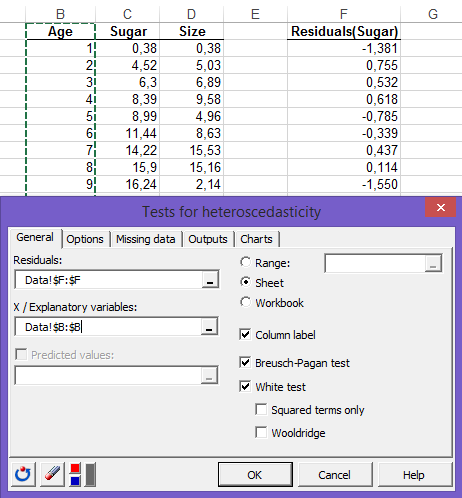
同じ手順を残差ボックスで残差(Size) の列を選択して繰り返します。

解釈

変数Sugar content については、残差 / Age のチャートが、変数Ageに対する残差の相対的な均一分散を示します。

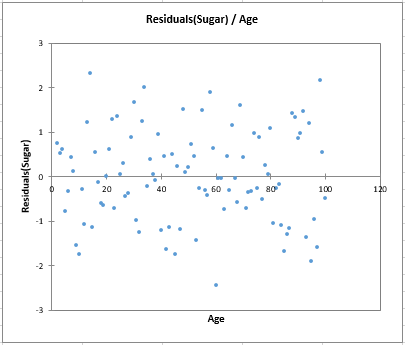
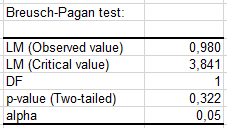
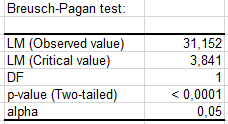
さらに、2つの検定が高いp値（Breusch-Pagan検定では0.322、 White検定では0.296）を示し、残差が均一分散であるという帰無仮説を棄却できないことを示します。

変数Sizeについては、 残差 / Age のチャートが、残差のフルーツの成長に伴って、よりばらつくことを明らかに示します。このようなコーン型の形は、不均一分散のとてもよくあるケースです。

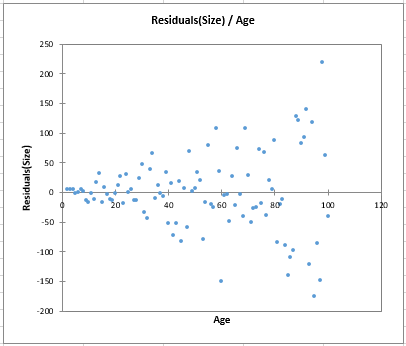
さらに、2つの検定の p値が 0.05の有意水準よりもかなり低いことがわかります。 したがって、我々は、チャートによって示唆されることとも一致して、残差が均一であるという帰無仮説を棄却しなければなりません。

追加情報: このチュートリアルのデータセットが生成された方法

従属変数Sugar content は、変数Ageの2倍とゼロを中心としたランダム正規誤差の合計で作成されています。 この誤差が残差を表現しています。 これは、残差が独立で一様分布する典型例です。2番目の従属変数 (Size)については、残差がAgeとランダム正規誤差の積になっています。この場合、残差は明らかに独立ではありません。より詳細は、チュートリアルのデータセットに含まれるadditional info シートをご覧ください。