混合モデルを用いた非釣り合いデータによる反復測定ANOVA

このチュートリアルは、XLSTATを用いてExcel内でデータが非釣り合いの場合の混合モデル を用いて反復測定分散分析をセットアップして解釈する方法を説明します。

データセット

データは2つの群に分けられた24人の患者で異なる時間に測定されたうつ病スコアの評価です。2つの群とは、処置群と処置を行わなかった対照群です :

• Subject: この質的変数は患者の識別子を格納します。
• Group: この質的変数は、患者が属する群を知ることができるようにします (1: 処置群 / 2: 対照群)。
• Time: この質的変数は、いつスコアの測定が行われたかを示します。5個のモダリティがあります (0: 処置開始前、1: 処置開始1ケ月後、3: 3ケ月後および 6: 6ケ月後)。
• dv: 量的従属変数は患者のうつ病の状態を評価するスコアを表します。

データは非釣り合いです。すなわち、少なくとも1個の因子のモダリティの数が等しくありません。 たとえば、subject 1 は、時間 6 で測定されていませんが、subject 2 は測定されています。

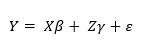反復測定ANOVA は、統的なANOVAと同じモデルに基づきます。我々の事例では、モデルの式は次のように書けます: したがって、我々は2個の混合要因 (変数 "group" と"time") および交互作用 ("group * time")を持ちます。従来の分散分析との違いは、eijk 誤差が相関し得ることです。実際、我々は異なる時間に同じ患者で行われた測定が独立であると仮定することができません。 混合モデルでは、モデル式は次式で与えられます: ここでYは説明されるべき量的変数で、Xは固定効果に関連する因子を収集します (これらは線形回帰の伝統的な変数です)。 β は固定効果に関連する係数のベクトルです。Z は変量効果を収集する行列です（iこれは固定であると仮定できない変数です）、γは変量効果に関連する係数のベクトルで、ε は各オブザベーションに関連する誤差です。 混合モデルによる反復測定ANOVAを再現するための1つの解決策は、subject 因子を（分散成分共分散構造を持つ）ランダム変数として含め、同じプロパティで誤差共分散構造を宣言することです。

複雑な共分散構造や我々の事例のように非釣り合いデータを持つ混合モデルでは、固定効果の検定統計量が未知の分布に従い、もはや正確F (Fisher) 検定ではありません。検定統計量が、ほぼ F 分布に従うと仮定して、問題のモデルの各固定効果の有意度を検定するために、XLSTATは誤差項のランダム誤差源の適切な線形結合を見つけて残差の近似 (Satterthwaite -1946)を実装します。

混合モデルを用いた反復測定ANOVA のセットアップ

XLSTATを開いて、XLSTAT / データモデリング / 混合モデル コマンドを選択するか、データモデリングツールバーの対応するボタンをクリックしてください（下図）。 ボタンをクリックすると、混合モデルダイアログボックスが現れます。Excel シートでデータを選択してください。 従属変数 は説明される変数（モデルされる変数）で、この事例ではscore (dv)です。残りのすべての変数は、質的説明変数です。3個の変数"subject"、"time"、"group"を選択してください。 列の最初の行が変数の名前を格納しているので、変数ラベルオプションが有効にされています。

オプションタブで、誤差と変量効果gの共分散行列構造を選択できます（詳細はXLSTATヘルプを参照）。 変量効果の分散成分構造を選択してください（残差は同じデフォルトの共分散構造を持ちます）。我々は制約 a1 = 0を選びます。これは、我々が対照群がスコアで標準の効果を持つという仮定でモデルを構築したいということを意味します。ANOVA での制約の適用は、理論的理由から不可欠ですが、分析の結果や品質を変えることはありません。 さらに、我々は交互作用を考慮に入れるので、交互作用オプションを有効にしなければなりません。 我々は Satterthwaiteのt検定 オプションも有効にして、モデルの誤差項にSatterthwaite近似を使用します。

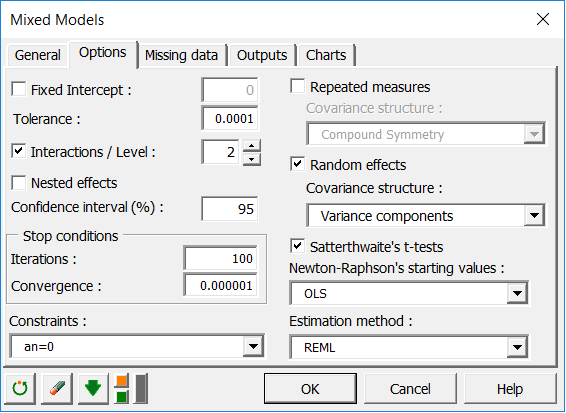OKをクリックすると、新しいウィンドウが表示されて、固定効果と変量効果を選択できます:

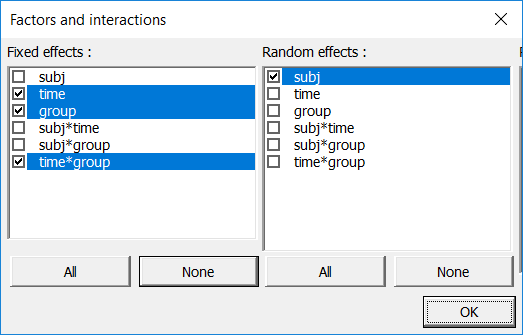我々は、"time"、"group"および交互作用 "time*group" を固定効果として、そして"subject" 変数と変量効果として用いて、反復測定ANOVAを実行します。 OK ボタンをクリックすると、計算が開始します。そして結果が表示されます。

混合モデルを用いた非釣り合い反復測定ANOVAの結果の解釈

XLSTATによって表示される最初の結果は、適合度係数です。

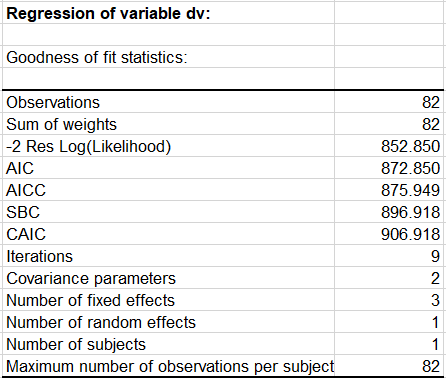モデル・パラメータは、制限付き最尤推定法(REML) を用いて得られ、伝統的な ANOVAモデルが適用される場合とは異なります。すべての指標が、モデルをさまざまな共分散構造と比較するのに使用されます。

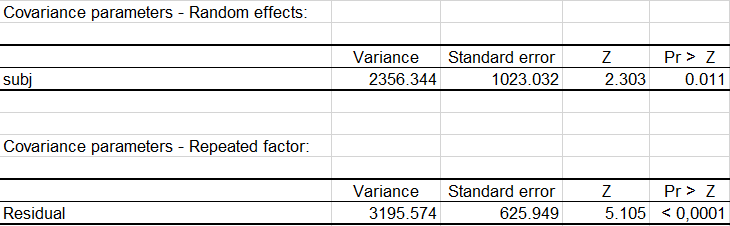
続く表は、変量効果と誤差の共分散行列のパラメータ (分散成分構造)を与えます。Z検定のp値 (Pr> Z) は、下の表で、モデルのランダム・パラメータの標準誤差推定の信頼性が良いことを示しています。ただし、標本サイズが小さいので、パラメータの標準誤差が大きいことに注意してください。

固定効果のタイプ III 検定の表（下図）は、FisherのF検定を用いて固定効果の有意度を確認できるようにします。ここで我々は、すべての固定効果が有意であることがわかります。経過時間が最も重要な効果を持ちます。 分母の自由度を計算するのにSatterthwaite近似法が使用され、正確な値 (Pr> F) を計算して、検定される仮説（"最小2二乗平均"の差の同等性）でのタイプIエラー（第1種の過誤）を減少させるために、F統計量が使用されます。

非釣り合いデータのケースでは、高次の項の検定（ここでは"group time" 交互作用）は常に同じですが、一方、低次の項("time" および"group")のタイプの間では仮定が異なります。我々の事例では、典型的な仮説 I と II は、各因子-水準の組み合わせでのオブザベーション（実験単位）の数に依存するため、これらのタイプの仮定は解釈しにくくなります。

それに対して、タイプIII仮説検定は、データが釣り合っているかどうかに関係なく、非釣り合いデータセットの調査に適した特性を提供する他の要因の効果を制御することによって（直交分解を介して）、常に考慮される固定効果を検定します。 したがって、処置（グループ変数）と経過時間は患者のうつ病のレベルに影響を与えると結論付けることができます。

次の表は、モデル・パラメーターとその標準偏差と信頼区間をまとめたものです。 パラメータの解釈は、古典的な分散分析の場合と同様です。 以下では、回帰係数の非ヌルに関するStudentのt検定は、Studentの法則に厳密には準拠していません。 ただし、以下の表に示されている結果は、誤差項の有効自由度に対するSatterthwaite 似に基づいた帰無仮説の下でのStudentt分布を近似しています。

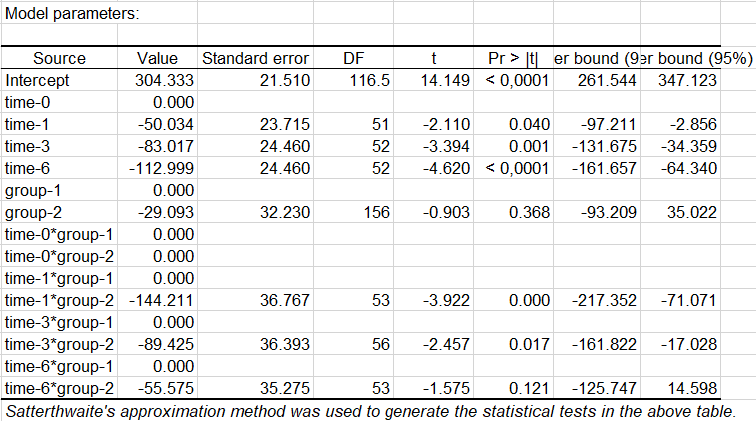
モデル・パラメーターを見ると（以下を参照）、時間1、3、および6がうつ病スコアにマイナスの影響を与えていることがわかります。 時間が経つにつれて、患者は落ち込んでいきます。 処置群であることも、うつ病スコアにマイナスの影響を与えます。

したがって、データセットが必要な条件（被験者ごとの厳密に同一の反復回数）を満たしていないにもかかわらず、混合モデルで反復測定ANOVAを実行することができました。 さらに、Satterthwaiteのモデル誤差項への近似により、異なる計算された統計的テストの信頼性の高い結果が保証されます。 （タイプI、II、III、およびt検定）。