Excelでの平均、中央値、標準偏差など

このチュートリアルは、XLSTATソフトウェアを用いてExcelで量的データの平均、中央値、標準偏差およびその他の記述統計量を計算して解釈する方法を示します。

量的データを説明するデータセット

データと結果のExcelシートは、以下のボタンをクリックしてダウンロードできます：

データをダウンロード

データは、人々がオンライン・ショッピンで出費する金額を月平均で調査した結果を示します。行が回答者で、列が費やす金額および彼らが属する年齢グループに対応します。 ここでの我々の目的は、以下のような一般的な記述統計量を用いて、年齢グループごとに結果を要約することです： 1. 中心傾向を反映する平均および中央値 2. バラツキを反映する標準偏差、分散および変動係数。

これは、調査から重要な情報を抽出して、グループ間の潜在的な差を検出することを可能にします。

記述統計量のダイアログ・ボックスのセットアップ

1. XLSTATを開いて、 以下に示す XLSTAT / データ記述 / 記述統計 コマンドを選んでください。 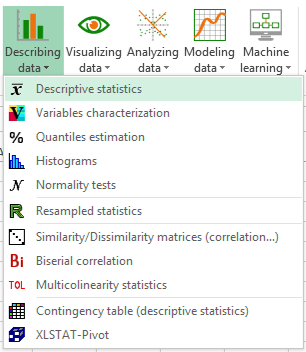2. 記述統計ダイアログ・ボックスが現れます。 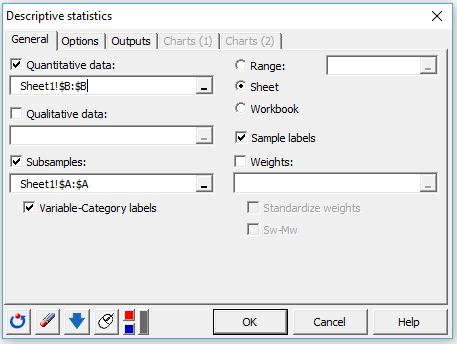3. 一般タブの量的データフィールドで、オンライン・ショッピングに費やす金額に対応する列を選んでください。

そして、副標本フィールドで、年齢クラスに対応する列を選択してください。

我々は、また出力に変数-カテゴリ・ラベルを表示させたいとします。これらは、変数名を接頭ｍカテゴリ名を接尾に含みます。

最後に、結果を新しいシートに表示させるためにシートオプションを選び、データ・テーブルの最初の行をラベルとみなすために標本ラベルを選びます。

4. オプションタブでは、以下のオプションを有効にします：

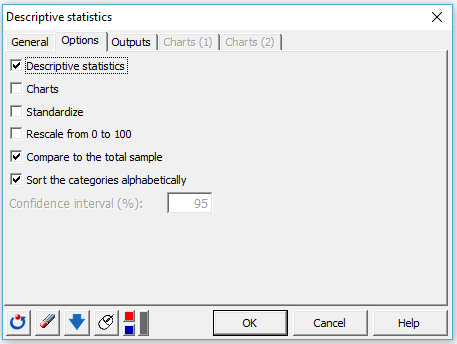
このチュートリアルで、我々は記述統計量に注目することとし、チャートは有効にしないことにしておきます。

我々は単一の変数のみを取り扱っているので、正規化または再尺度化オプションは選びません。それは、異なる尺度で計測された複数の変数の場合に役立ちます。

5. 出力タブで、量的データのすべての統計量を選択するために、すべてボタンをクリックします。

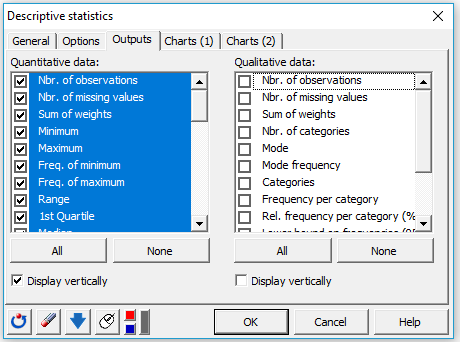## 量的データの記述統計量の解釈

結果はDescと名付けられた新しいシートに表示されています。すべての回答者について（列B)および年齢クラスごとに（C-E）、記述統計量のフルセットが表示されています。

最もよく使用される基本の統計量は、データの中心部分の情報を提供する中心傾向の測度（すなわち、平均、中央値）、およびデータの変動を説明するバラツキの測度（すなわち、標準偏差、範囲、分散、変動係数）です。

XLSTATのヘルプ・メニュー（ダイアログ・ボックスでヘルプ・ボタンをクリック）に定義と数式が書かれています。

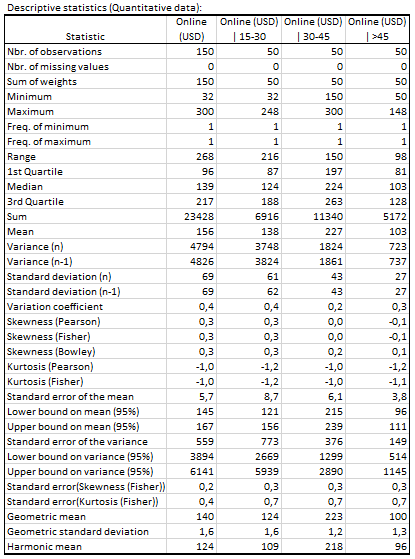
a. 中心傾向の解釈

平均は、回答者たちが全体的にオンライン・ショッピングで月で均して、156 USD 費やしていることを示します。

中央値は 139 USDです。これは、回答者の半分が 139 USD より多く費やしており、その他の半分が139 USDより少ないことを意味します。中央値が平均値よりもわずかの低いので、データは右に偏っているようです。

3つの年齢グループを見渡して、我々は30歳から 45歳の間の年齢の消費者が他の2つのグループよりも平均でより費やしていることを観察します（平均および中央値）。 1つの解釈は、この年齢カテゴリの人々は、高齢クラスよりもテクノロジーによりこだわる若年カテゴリよりも 、支出できるお金をより多く持っているということのようです。

b. バラツキの解釈

若い顧客は最も高齢な顧客 (>45)よりも平均でより出費しているようですが、彼らはより高い標本標準偏差(SD = 62)を持ちます。これはカテゴリ (>45)と比較してカテゴリ(30-45) が出費する金額の範囲がより広いことを意味します。同様に、より高齢な人々は同じような金額 (低い SD)を出費する傾向があると言えます。さまざまな説明が可能です。たとえば、若年の購買者は高齢者よりも多様な社会的職業カテゴリ（学生、就業、無職）を含んでいると言えます。

これらの結論も分散に基づいて引き出されます。分散の代わりにSDを用いる利点は、 SDが元の尺度の単位を用いることです。

バラツキのもう1つの測度は、変動係数です。これは単位がつけられていないので、さまざまな単位で標本を比較するときに使用すると、とくに役立ちます。変動係数が高いほど、平均のまわりのバラツキのレベルがより高くなります。

標準偏差 (n) か標準偏差 (n-1) か?

このチュートリアルで、我々は母数段を調査するための標本として、150人の回答者を用いています。 これは解釈のために標本 SD (n-1) を使用する我々の選択を説明します。オンラインでショッピングするすべての人々（すなわちオンライン購買者の母集団）のデータを収集することが理想ですが不可能なので、母集団 SD [標準偏差 (n)] または 母集団分散 [分散 (n)] はより近似的になります。

次にするべきこと: 箱ひげ図による量的変数の記述

量的変数をグラフィカルに記述する素早く簡単な方法をお探しですか? 箱ひげ図がぴったりです。このツールは、全体データでもグループごとでも、5つの基本統計量（最小、第1四分位、中央値、第3四分位、最大）を一目でわかるように提供します。 こちらで我々の箱ひげ図およびノッチつき箱ひげ図のチュートリアルをご覧ください。