Excelでのヒストグラムと分布の適合チュートリアル

このチュートリアルの目的は、Excel内でXLSTATの分布の適合ツールを使用して、ヒストグラム を生成して、ある標本が負の二項分布に従うかどうかを検定することです。この分布は、水環境でのバクテリアの凝集/分散現象を表現するためによく使用されます。

ヒストグラムを作成して分布を適合するデータ

データと結果のExcelシートは、上のリンクでダウンロードできます。

データは、大腸菌による細菌汚染の有無を決定するために、河川からの水の200サンプルが養分つきの培地で培養された実験です。コロニーの数は、72時間の培養後にカウントされています。Bact-Dataの列には、200サンプルのカウントが表示されます。

ヒストグラムを作成するためのダイアログ・ボックスのセットアップ

XLSTATを開いて、XLSTAT / データ可視化 / ヒストグラム コマンドを選択してください（下図参照）。 below).

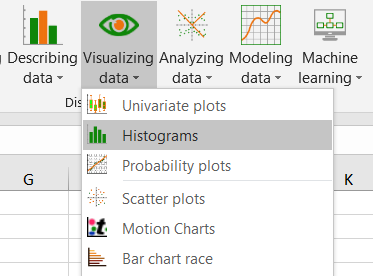
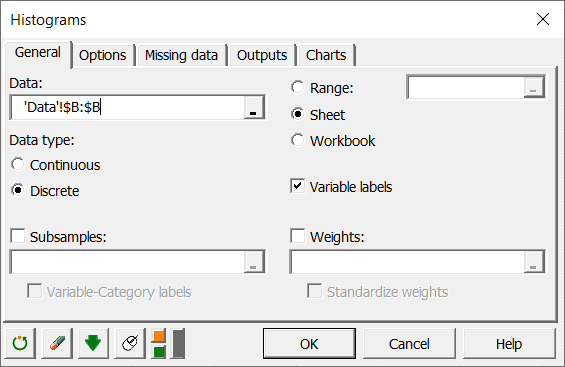
そして、ダイアログ・ボックスが表示されます。Dataと名付けられたExcelシート上のデータを選択します。 一般タブで、データ・フィールドのB列を選択します。 カウントは離散値なので、離散オプションを有効にします。データ選択の最初の行にサンプルの名前が含まれているため、標本ラベル・オプションは有効なままにしておきます。

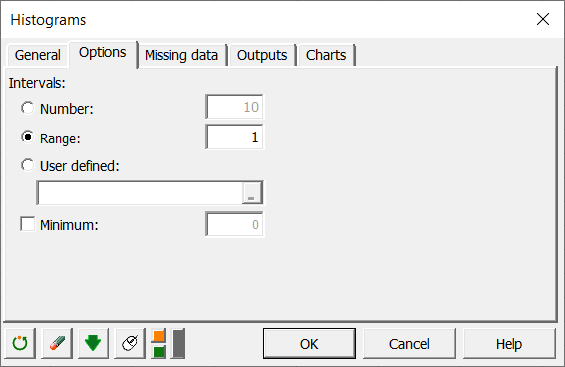
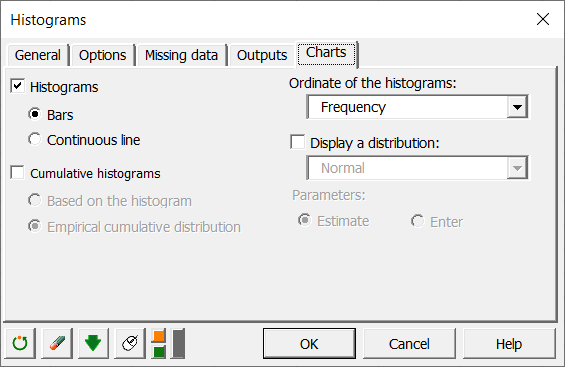OK ボタンをクリックして計算が立ち上がります。そして、新しいシートに結果が表示されます。

ヒストグラムの解釈

シートHistogramの要約統計の表の下にヒストグラムが表示され、その後にヒストグラムの統計が得られる表が続きます。

ヒストグラムでは、最も度数の高い値が0であり、データの20％以上を占めていることがわかります。つまり、5個のサンプルのうち1個以上のサンプルで細菌が発見されていません。また、度数が急速に減少していることにも気づきます。1個のサンプルでは、36個以上のコロニーがカウントされました。

区間の境界を指定してヒストグラムを作成

我々は負の二項分布関数と標本の間の適合を検定したいので（カイ2乗検定は、1個のクラスに少なくとも5個のデータがあることを要求します）、また、バクテリアのカウントの精度が不確かなので、カウントをより大きなクラスにグループ化する必要があるように思われます。この理由から、我々の問題と一致すると思われる境界値のリストを作成しました：0,1,2,3,4,5,10,15,20,40。 新しいクラスの度数が5より大きく、規則的に減少しているかどうかを確認するために、今回はオプション・タブで区間の境界を指定して、新しいヒストグラムを作成します。

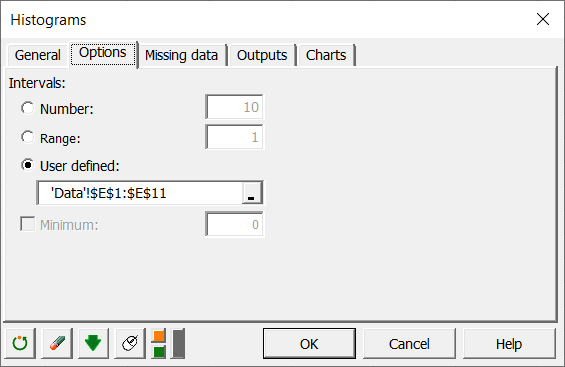OKボタンをクリックすると計算が始まり、新しいヒストグラムが現れます(シート"Histogram1"を参照)。

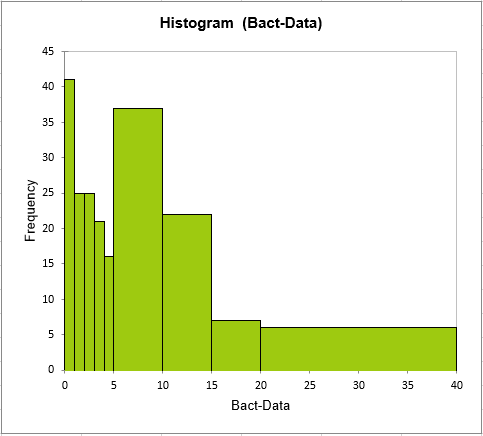我々はこの結果に満足なので、標本が負の二項分布に従うかどうかを検定するために、分布の適合ツールを使用することができるようになりました。

分布を適合するためのダイアログ・ボックスの設定

XLSTAT / データ・モデリング / 分布の適合コマンドを選択してください（下図参照）。

そして、分布の適合ダイアログ・ボックスが現れます。Dataという名前のExcelシートを選択してください。

一般タブで、データ・フィールドに列Bを選択してください。我々は XLSTATに負の二項分布関数のパラメータを推定させます。 XLSTATは、負の二項分布の2種類の式を提供します。我々の事例に適応するのは、2番目のものです。

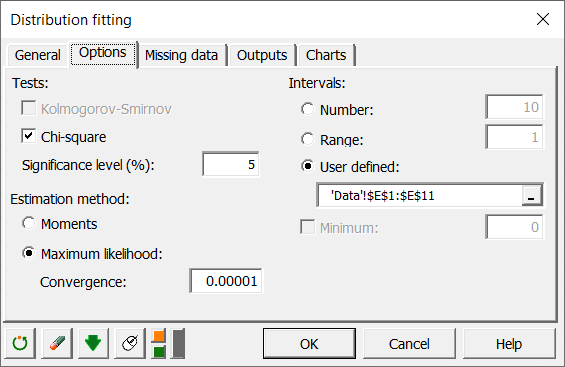
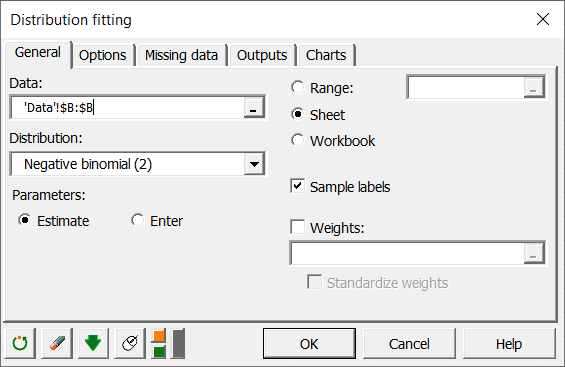オプション・タブで、 我々の仮定を検定するのに必要なカイ2乗適合度検定を有効にします。我々は上記で定義した境界を使用します。

チャート・タブで以下のオプションを選択します。

## 分布の適合分析の結果の解釈

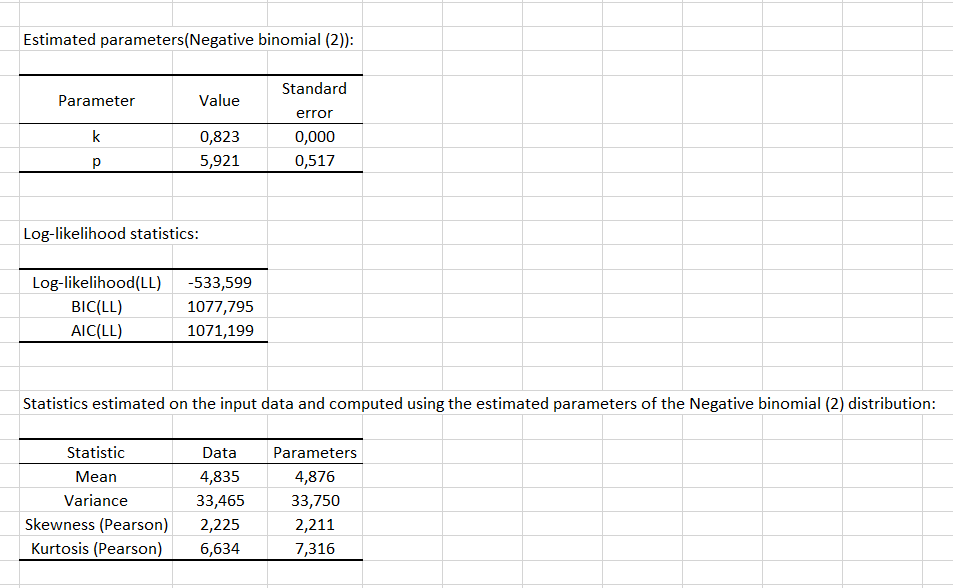
我々が興味を持つ最初の結果は、負の二項分布（最尤法を用いて適合）のkおよびpパラメータの値と、標本と理論的な平均、分散、歪度、尖度の推定値です。これらの統計量がデータとパラメータから得られるものに近いほど、適合が良好です。ここでは、適合は優れています。注意: 理論平均は kp、分散は kp(p+1) で与えられます。

カイ2乗適合度検定は、経験分布関数と理論的分布関数の間のカイ2乗距離が臨界値を超えているかどうかを検定することができます。観測度数と理論度数の間の視覚的な比較は、次の図で見ることができます。 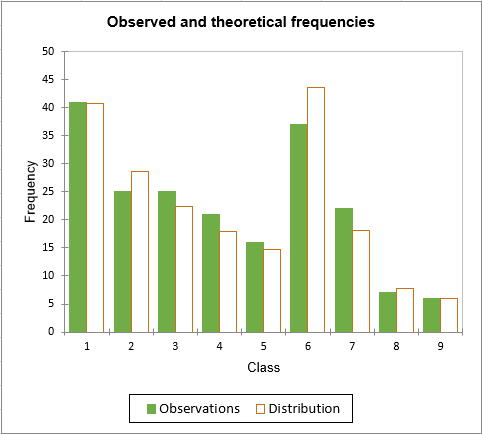クラス2, 6, 7については、わずかな違いがあるようです。このわずかな差にもかかわらず、検定のために計算されたp値(0.770)は、我々が選んだ有意水準(0.05)よりも有意に高いです。したがって、カイ二乗検定は、データが負の二項分布に従うという我々の仮説を確認します。 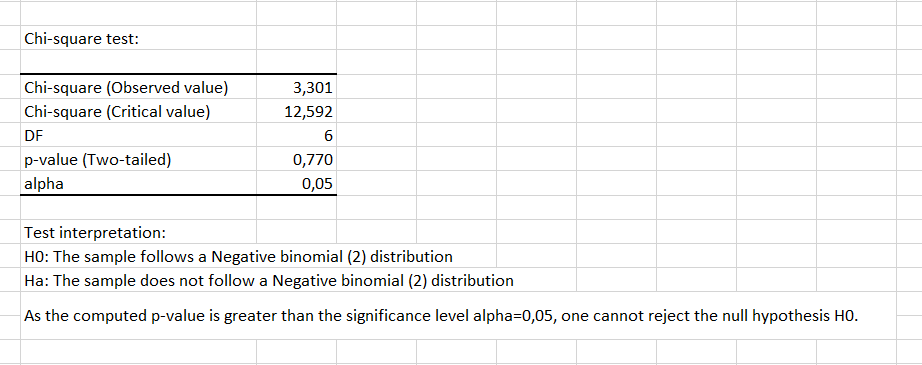結論として、サンプルが採取された河川における関心のある細菌の存在は、平均値が4.8、分散が33.4の負の二項分布（k=0.823、p=5.921）に従っています。