Qn 統計量を計算する際に使用する定数の補正，高破綻によるロバスト尺度推定量

下記の表に，Croux and Rousseeuw (1992)で定義されているdn定数のリストをあげる．これらの著者が示した初期値は，式6の誤植によるものである; 定数 2.2219 は 2.2191だったはずである．ちなみに，定数の値は次式に対応する:

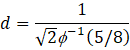
ここで f -1 は， 逆標準正規分布関数である．この誤りは，Rousseeuw and Croux (1993) および，version 2015まで，ISO 13528 標準を含む，その後の多くの論文や文書で再生産された．さらに，初期 dn 定数は，10000回のシミュレーションを用いて推定されていた．我々は，定数の推定値の分散を考慮すると，小数第一位以下のすべての桁について十分な信頼性を得るためには，シミュレーションの回数が不足していたことを確認した．

我々がXLSTATにもたらしている改善について:

• n=2では，定数は解析的に計算できる．桁は確実である．
• nが3から12でのdn値は，109 回のシミュレーションを用いて推定されている．
• nが13から40でのdn値は，108 回のシミュレーションを用いて推定されている．
• nが41から10でのdn値は，107回のシミュレーションを用いて推定されている．

次の表は， [3, 100]のnでのf dn の推定値，および dnの分散の推定値，およびdnの第4桁で持ち得る信頼度を一覧する． | n | dn | stdev(dn)** | Conf(%)** | |---|---|---|---| | 2 | 0.3994 | | 100 | | 3 | 0.9936 | 2.6627 x 10-5 | 88 | | 4 | 0.5122 | 1.2789 x 10-4 | 30 | | 5 | 0.8397 | 2.8902 x 10-5 | 77 | | 6 | 0.6055 | 5.9362 x 10-5 | 50 | | 7 | 0.8569 | 2.0620 x 10-5 | 89 | | 8 | 0.6674 | 3.6643 x 10-5 | 56 | | 9 | 0.8706 | 1.6333 x 10-5 | 59 | | 10 | 0.7198 | 2.5437 x 10-5 | 60 | | 11 | 0.8889 | 1.3343 x 10-5 | 98 | | 12 | 0.7574 | 1.9510 x 10-5 | 84 | | 13 | 0.9024 | 3.6098 x 10-5 | 69 | | 14 | 0.7855 | 5.0419 x 10-5 | 51 | | 15 | 0.9126 | 3.1790 x 10-5 | 85 | | 16 | 0.8078 | 4.2796 x 10-5 | 67 | | 17 | 0.9210 | 2.8565 x 10-5 | 53 | | 18 | 0.8260 | 3.0824 x 10-5 | 75 | | 19 | 0.9280 | 2.4156 x 10-5 | 50 | | 20 | 0.8410 | 2.7943 x 10-5 | 93 | | 21 | 0.9340 | 2.2428 x 10-5 | 74 | | 22 | 0.8535 | 2.5641 x 10-5 | 75 | | 23 | 0.9391 | 2.0992 x 10-5 | 94 | | 24 | 0.8644 | 2.3767 x 10-5 | 56 | | 25 | 0.9432 | 1.9776 x 10-5 | 97 | | 26 | 0.8737 | 2.2207 x 10-5 | 75 | | 27 | 0.9468 | 1.8729 x 10-5 | 63 | | 28 | 0.8820 | 2.0897 x 10-5 | 60 | | 29 | 0.9500 | 1.7826 x 10-5 | 97 | | 30 | 0.8889 | 1.9755 x 10-5 | 99 | | 31 | 0.9533 | 1.7043 x 10-5 | 96 | | 32 | 0.8952 | 1.8774 x 10-5 | 97 | | 33 | 0.9556 | 1.6336 x 10-5 | 94 | | 34 | 0.9009 | 1.7914 x 10-5 | 85 | | 35 | 0.9579 | 1.5709 x 10-5 | 54 | | 36 | 0.9058 | 1.7145 x 10-5 | 96 | | 37 | 0.9600 | 1.5149 x 10-5 | 98 | | 38 | 0.9105 | 1.6468 x 10-5 | 100 | | 39 | 0.9618 | 1.4636 x 10-5 | 92 | | 40 | 0.9148 | 1.5856 x 10-5 | 80 | | 41 | 0.9637 | 4.6517 x 10-5 | 72 | | 42 | 0.9187 | 5.2677 x 10-5 | 61 | | 43 | 0.9652 | 4.5065 x 10-5 | 73 | | 44 | 0.9220 | 5.0759 x 10-5 | 62 | | 45 | 0.9667 | 4.3716 x 10-5 | 74 | | 46 | 0.9252 | 4.9036 x 10-5 | 63 | | 47 | 0.9678 | 4.2481 x 10-5 | 54 | | 48 | 0.9280 | 4.7425 x 10-5 | 56 | | 49 | 0.9692 | 4.1354 x 10-5 | 69 | | 50 | 0.9307 | 4.5949 x 10-5 | 72 | | 51 | 0.9704 | 4.0284 x 10-5 | 74 | | 52 | 0.9331 | 4.4611 x 10-5 | 57 | | 53 | 0.9715 | 3.9302 x 10-5 | 57 | | 54 | 0.9357 | 4.3356 x 10-5 | 75 | | 55 | 0.9725 | 3.8388 x 10-5 | 71 | | 56 | 0.9378 | 4.2217 x 10-5 | 53 | | 57 | 0.9732 | 3.7518 x 10-5 | 52 | | 58 | 0.9397 | 4.1137 x 10-5 | 66 | | 59 | 0.9744 | 3.6713 x 10-5 | 78 | | 60 | 0.9418 | 4.0133 x 10-5 | 53 | | 61 | 0.9750 | 3.5967 x 10-5 | 52 | | 62 | 0.9436 | 3.9202 x 10-5 | 52 | | 63 | 0.9757 | 3.5253 x 10-5 | 81 | | 64 | 0.9453 | 3.8341 x 10-5 | 79 | | 65 | 0.9765 | 3.4565 x 10-5 | 85 | | 66 | 0.9470 | 3.7503 x 10-5 | 56 | | 67 | 0.9770 | 3.3937 x 10-5 | 86 | | 68 | 0.9483 | 3.6736 x 10-5 | 52 | | 69 | 0.9776 | 3.3343 x 10-5 | 72 | | 70 | 0.9496 | 3.5991 x 10-5 | 57 | | 71 | 0.9782 | 3.2757 x 10-5 | 78 | | 72 | 0.9510 | 3.5309 x 10-5 | 63 | | 73 | 0.9788 | 3.2222 x 10-5 | 76 | | 74 | 0.9524 | 3.4649 x 10-5 | 60 | | 75 | 0.9794 | 3.1677 x 10-5 | 56 | | 76 | 0.9534 | 3.4031 x 10-5 | 86 | | 77 | 0.9800 | 3.1214 x 10-5 | 85 | | 78 | 0.9546 | 3.3438 x 10-5 | 67 | | 79 | 0.9804 | 3.0715 x 10-5 | 57 | | 80 | 0.9558 | 3.2884 x 10-5 | 53 | | 81 | 0.9809 | 3.0261 x 10-5 | 85 | | 82 | 0.9568 | 3.2341 x 10-5 | 87 | | 83 | 0.9815 | 2.9837 x 10-5 | 78 | | 84 | 0.9578 | 3.1834 x 10-5 | 79 | | 85 | 0.9819 | 2.9412 x 10-5 | 91 | | 86 | 0.9587 | 3.1337 x 10-5 | 85 | | 87 | 0.9821 | 2.9017 x 10-5 | 89 | | 88 | 0.9597 | 3.0871 x 10-5 | 55 | | 89 | 0.9826 | 2.8634 x 10-5 | 92 | | 90 | 0.9604 | 3.0417 x 10-5 | 90 | | 91 | 0.9831 | 2.8246 x 10-5 | 91 | | 92 | 0.9614 | 2.9994 x 10-5 | 70 | | 93 | 0.9832 | 2.7912 x 10-5 | 73 | | 94 | 0.9622 | 2.9560 x 10-5 | 76 | | 95 | 0.9837 | 2.7551 x 10-5 | 62 | | 96 | 0.9628 | 2.9175 x 10-5 | 86 | | 97 | 0.9842 | 2.7220 x 10-5 | 88 | | 98 | 0.9638 | 2.8795 x 10-5 | 66 | | 99 | 0.9842 | 2.6903 x 10-5 | 91 | | 100 | 0.9644 | 2.8415 x 10-5 | 92 |

高いnの数では，dn 定数は次のように推定される:

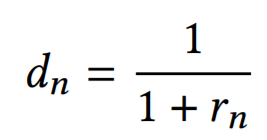
n>100 ここで n は奇数，では，

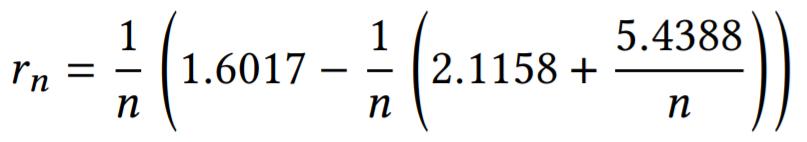
n>100 ここで n は偶数，では，

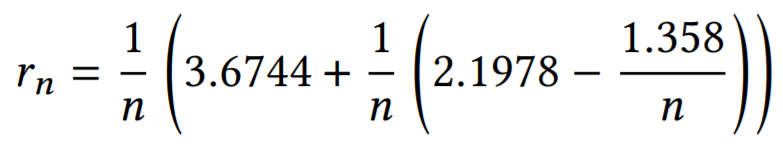
参考文献:

Croux C. and Rousseeuw P. J. (1992): Time-Efficient Algorithms for Two Highly Robust Estimators of Scale. Computational Statistics, 1, 411-428. ISO 13528, second edition 2015-08-01. Statistical methods for use in proficiency testing by interlaboratory comparison. Reference number ISO 13528:2015(E) Rousseeuw P.J. and Croux C. (1993). Alternatives to the Median Absolute Deviation. Journal of the American Statistical Association, 88, 1273-1283.