Gage R&R pour données quantitatives dans Excel

Ce tutoriel explique comment calculer et interpréter l'analyse Gage R&R pour des données quantitatives avec Excel en utilisant XLSTAT.

Jeu de données pour contrôler et valider une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

Un feuillet Excel contenant à la fois les données et les résultats peut être téléchargé cliquant sur le lien au-dessus.

Les données sont extraites d'une publication [Montgomery, D.C. (2001), Introduction to Statistical Quality Control, 4th edition, John Wiley & Sons].

Les données correspondent aux mesures sur un système avec 10 pièces et 3 opérateurs répétant chaque mesure 3 fois.

L'analyse de système de mesure des données quantitatives dans XLSTAT

Lorsque les mesures sont des données quantitatives, deux méthodes sont disponibles pour l'analyse Gage R&R. La première est basée sur l'analyse de variance (ANOVA) et la seconde sur les cartes de contrôle R (Amplitude et moyenne).

Dans les descriptions ci-dessous, σ²repeatability désigne la variance liée à la répétabilité. Plus elle est faible, plus la mesure est répétable (les opérateurs donnent chacun des résultats cohérents pour une même pièce). Le calcul de cette variance est différent en fonction de la méthode choisie (ANOVA ou carte de contrôle R). σ²reproducibility désigne la part de la variance correspondant à la reproductibilité. Plus elle est faible, plus la mesure est reproductible (les divers opérateurs donnent des résultats concordants pour une même pièce). Le calcul de cette variance dépend aussi de la méthode choisie (ANOVA ou carte de contrôle R)

σ²R&R est la variance du gage R&R. Elle est toujours la somme des deux variances précédentes : σ²R&R = σ²reproducibility + σ²repeatability.

Paramétrer un contrôle d'une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

Dans ce tutoriel nous utilisons la méthode d'analyse de la variance.

Une fois XLSTAT activé, sélectionnez la commande XLSTAT / SPC / Analyse du système de mesures (Gage R&R) / Quantitatives.

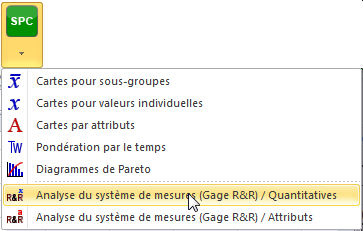
La boîte de dialogue Analyse du système de mesures (Gage R&R) / Quantitatives apparaît.

Sélectionnez les données dans l'onglet Général.

• Y / Mesures : colonne D,
• X / Opérateur : colonne A,
• Pièces : colonne B.

Choisissez aussi la méthode : ANOVA et activez les options Libellés des colonnes et Variables-Modalité ainsi que le tri alphabétique des modalités avant de changer d'onglet.

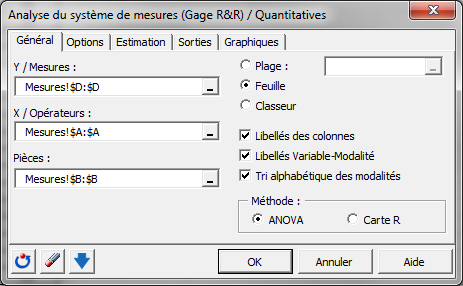
Dans l'onglet Options, enterez la valeur 6 pour le nombre de sigma utilisé pour la carte de contrôle. Choisissez aussi le plan croisé pour l'ANOVA.

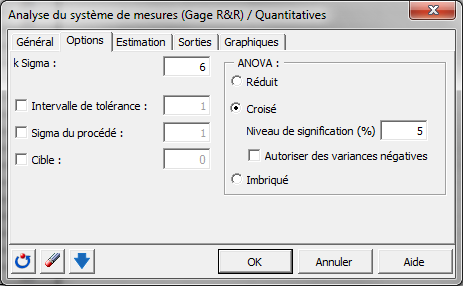
Dans l'onglet Estimation, choisissez l'option R-barre pour l'estimation de sigma.

Dans l'onglet Sorties, activez toutes les options.

Faîtes de même dans l'onglet Graphiques.

Lancez les calculs en cliquant sur OK.

Interpréter les résultats d'un contrôle d'une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

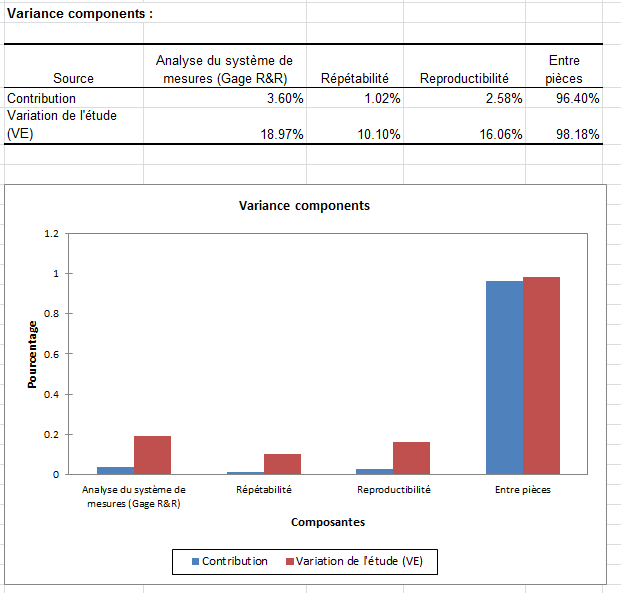
Les premiers résultats correspondent à "Variance components". La décomposition de la variance montre que la majeure partie de la variation est due à la variance entre pièces (96.40%). L'analyse du système de mesure quant à elle, n'est responsable que de 3.60% de la variance de l'échantillon. Ce système de mesure est donc capable.

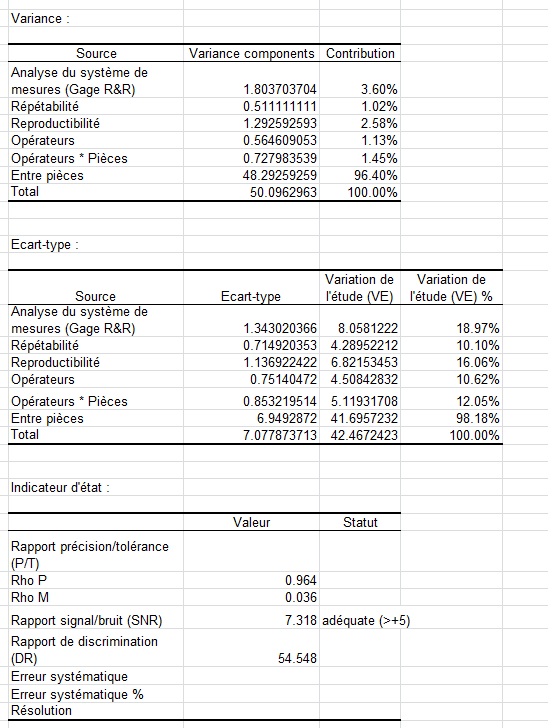
Les tableaux suivant présentent les détails de la décomposition de la variance et les indicateurs d'état obtenus sur ce système. On peut voir que le ratio Signal/Bruit est adéquat.

Comme nous avons sélectionné l'option "ANOVA" nous obtenons les résultats des coefficients d'ajustement et de l'analyse de la variance.

Regardez les valeurs des p-values. Tous les paramètres sont significatifs.

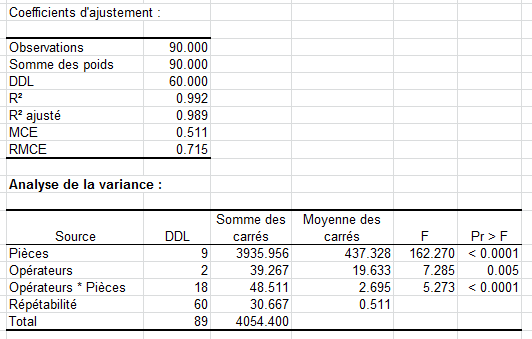
Après ces résultats vous trouvez les données qui permettent de construire la carte de contrôle X-barre, tout d'abord les limites de contrôle, puis les valeurs pour chaque échantillon.

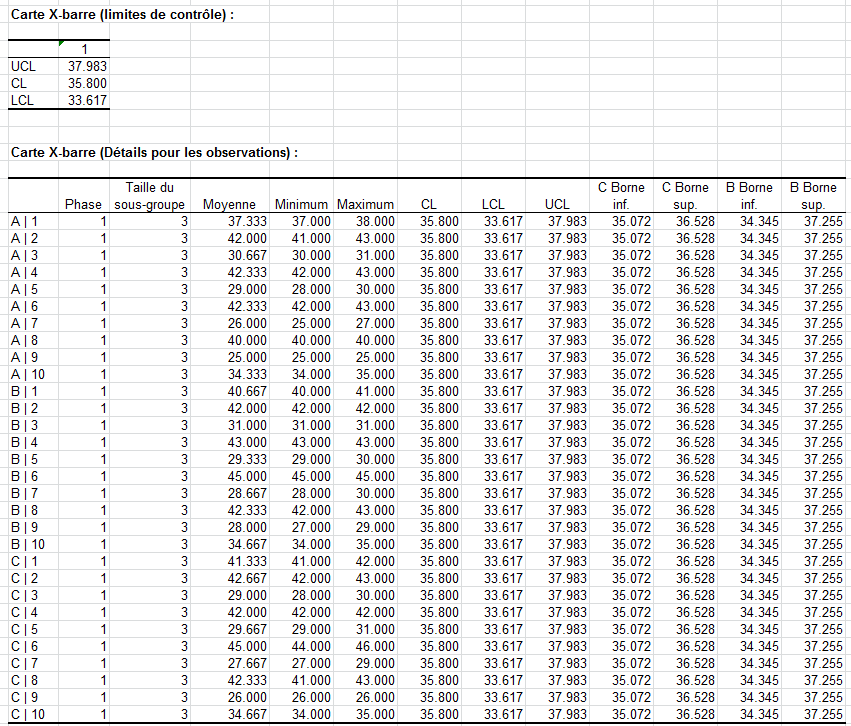
Puis vous avez la carte de contrôle. Vous pouvez voir que les moyennes pour chaque échantillon ne sont pas dans les limites de contrôles. La variance entre les pièces n'est pas sous-contrôle.

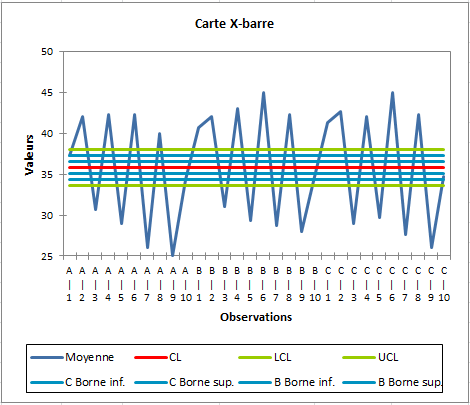
Pour la carte R, on trouve que les échantillons sont dans les limites de contrôle et aucune cause spéciale n'est détectée.

Ceci est un résultat typique pour ce type d'analyse.

Les deux cartes permettent de conclure que le système de mesure est capable et que la variance entre les pièces n'est pas sous-contrôle.

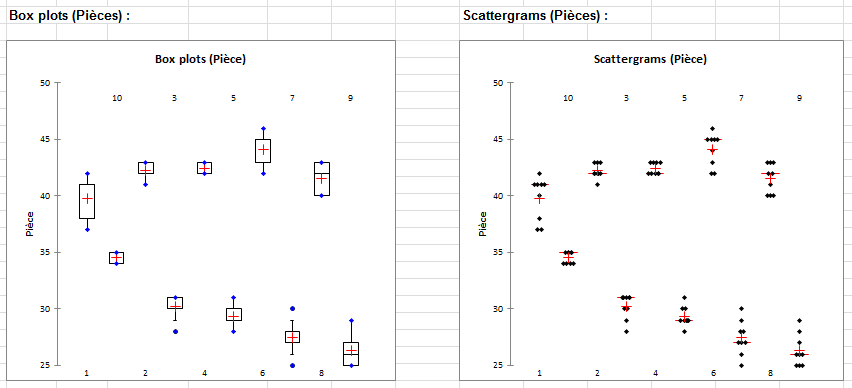
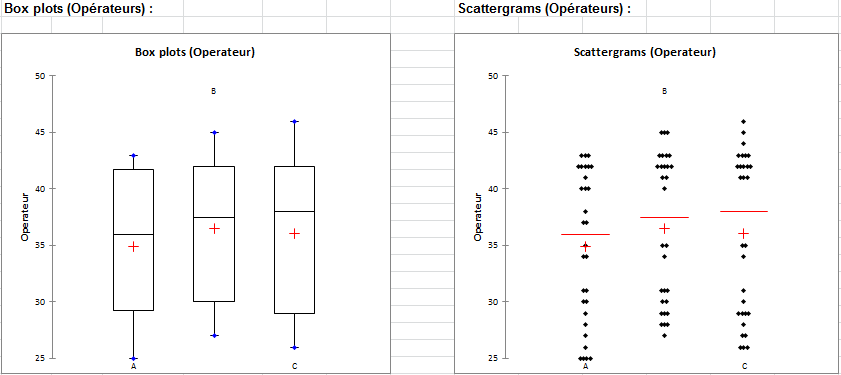
Vous pouvez visualiser la variance liée aux pièces et opérateurs en regardant les box plots et scattergrams associés à ces deux paramètres.

Pour les pièces les box plots sont très serrés ce qui montre une bonne répétabilité et reproductibilité des opérateurs. Il y a clairement 3groupes : pièces 2, 4, 6 et 8; pièces 3, 5, 7 et 9; et pièce 10.

La variance entre les opérateurs est très faible.

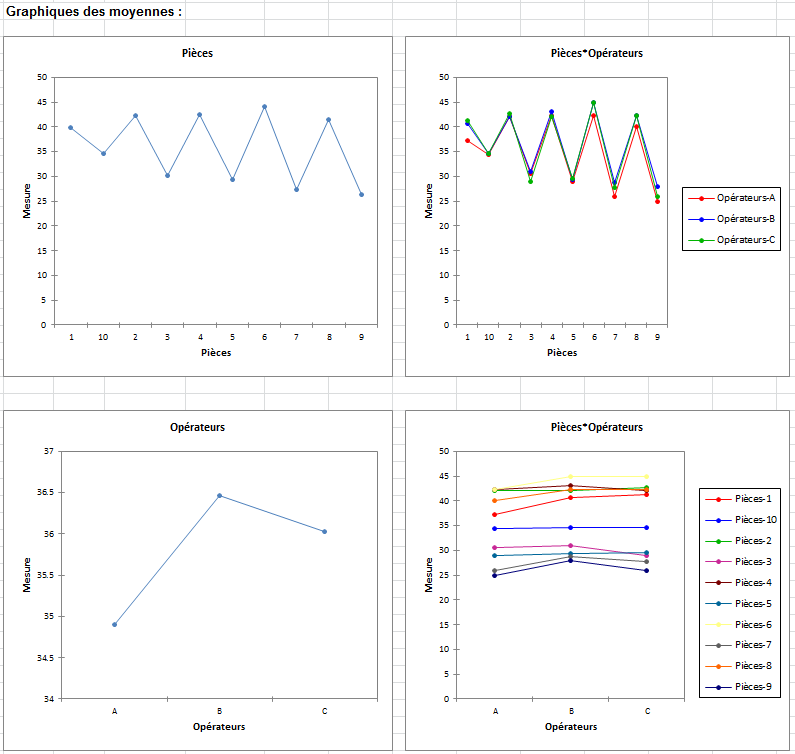
Enfin on peut visualiser les profils pour chaque pièce ou opérateur.

Les profils des opérateurs par pièce sont très semblables à part pour la mesure 1 et opérateur A.

Les profils des pièces par opérateur sont très plats indiquant une faible variation par opérateur mais varient beaucoup en intensité indiquant une forte variation pour chaque pièce.