Ajuster un modèle de Cochrane-Orcutt dans Excel

Jeu de données utilisé

Les données correspondent à l’exemple proposé dans le livre de Chatterjee et al. [Chatterjee, S., Hadi, A.S. and Price, B. (2000). Regression Analysis by Example, Wiley-Interscience Publication,John Wiley and Sons]. Il s’agit d’étudier la consommation des ménages (Expend) en fonction de leur épargne (Stock).

But de ce tutoriel

On suppose que le terme d’erreur dans la régression de entre Expend et Stock est généré selon un processus AR(1). Pour estimer les paramètres du modèle on utilise l’estimation de Cochrane-Orcutt.

Â

Paramétrer l’estimation de Cochrane-Orcutt

Une fois XLSTAT ouvert, sélectionnez la commande XLSTAT / XLSTAT-Time / Cochrane-Orcutt, ou cliquez sur le bouton correspondant dans la barre de menu.

La boîte de dialogue Cochrane-Orcutt apparaît.

Les données sont présentées sous forme d’un tableau constitué de 20 observations et de 2 variables. La variable Expend est la variable dépendante et Stock la variable explicative. L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.

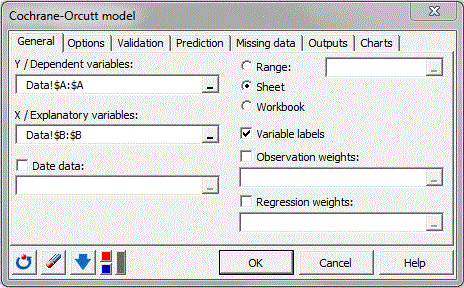
Dans l’onglet Options, il est possible de régler le seuil de tolérance ainsi que le niveau des intervalles de confiance. Nous choisissons ici de laisser les valeurs par défaut.

Lancez les calculs en cliquant sur OK. Les résultats sont affichés dans une nouvelle feuille Excel.

Interpréter les résultats

Les premiers résultats affichés sont les statistiques descriptives pour chaque variable. Ensuite vient le tableau des coefficients d'ajustement du modèle. Le R² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle.

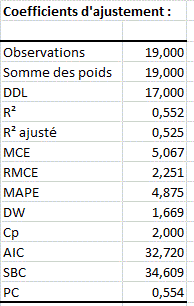
On trouve ensuite le tableau d'analyse de la variance (voir ci-dessous). C'est à ce niveau que l'on détermine si la variable explicative sélectionnée apporte une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser suffirait à décrire les résultats obtenus ou non.

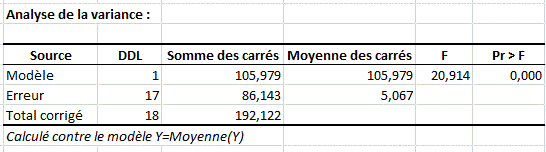
Les tableaux suivants fournissent les détails sur le modèle (paramètres, écart-type, …) ainsi que le coefficient d’auto corrélation rho. Ces tableaux sont essentiels dès lors que le modèle doit être utilisé pour faire des prévisions, des simulations ou s'il doit être comparé à d'autres résultats.

On dispose ensuite d’outils permettant d’analyser les résidus du modèle tels que le graphique des résidus centrés réduits. Ce graphique permet de repérer rapidement et visuellement la présence de valeurs hors de l'intervalle [-2, 2].

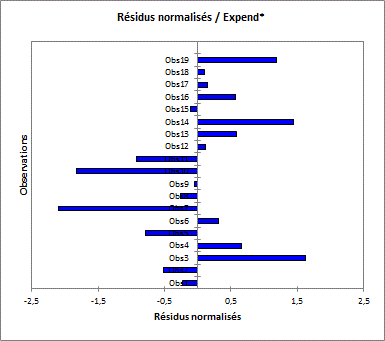
Ici, une seule des valeurs sort de l’intervalle.