Séries temporelles, analyse descriptive et transformation

Jeu de données pour l'analyse descriptive et transformations de séries temporelles

Les données proviennent de [Box, G.E.P. and Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco], et correspondent au trafic aérien international (en milliers de passagers) de Janvier 1949 à Décembre 1960.

Le but est ici d'analyser la série chronologique avant de l'utiliser en mode prédictif dans un autre tutoriel.

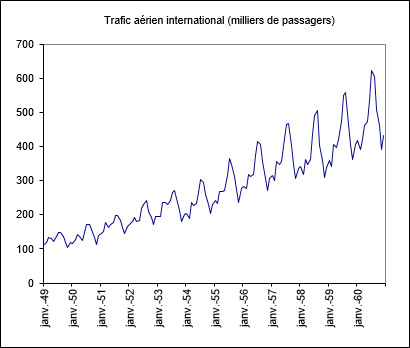
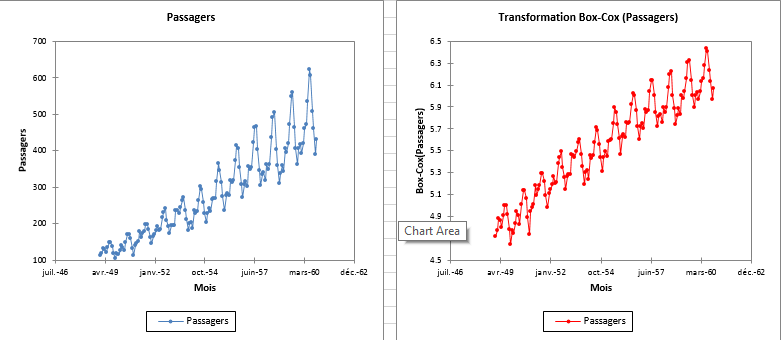
On note sur ce graphique que le nombre de passagers a tendance à augmenter régulièrement que l'on retrouve chaque année un cycle similaire. Cependant les variations à l'intérieur d'une même année sont de plus en plus fortes. Afin de confirmer ces éléments nous allons analyser la série, puis la transformer pour valider nos hypothèses.

Paramétrer une analyse descriptive de séries temporelles

Pour activer la boîte de dialogue de l'analyse descriptive des séries chronologiques, lancez XLSTAT, puis sélectionnez la commande XLSTAT / Time / Analyse descriptive.

Une fois que vous avez cliqué sur le bouton, la boîte de dialogue de l**'analyse descriptive** apparaît. Sélectionnez alors les données sur la feuille Excel. La série à analyser correspond ici à la série Passagers.

L'option Libellés des séries est activée parce que la première ligne des données sélectionnées correspond au nom de la variable.

Dans l'onglet Options, sélectionnez le mode automatique.

Dans les onglets Sorties et Graphiques, activez l'option Autocorrélations partielles.

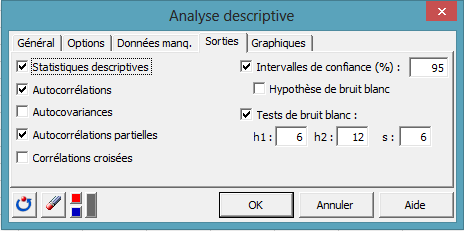
Les calculs commencent lorsque l'on a appuyé sur OK. Les résultats sont ensuite affichés.

Interprétation de l'analyse descriptive de séries temporelles

Dans les premiers tableaux sont affichées des statistiques générales.

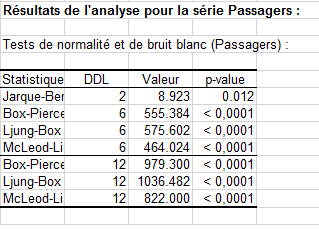
Ensuite, un tableau donne les résultats des tests de normalité et de bruit blanc.

Le test de Jarque-Bera est un test de normalité fondé sur les propriétés de symétrie et d’aplatissement de la loi normale. Plus la valeur du Khi² est importante, moins l'hypothèse nulle de normalité des données est vraisemblable. Ici, la probabilité fournie, qui correspond à la probabilité de se tromper en rejetant l'hypothèse nulle, est proche de 0,012. Avec un seuil de signification alpha=0.05, on doit donc rejeter l'hypothèse nulle.

Les trois autres tests (Box-Pierce, Ljung-Box, McLeod-Li) sont calculés à différents pas de temps. Ils permettent de tester si les données pourraient provenir d'un bruit blanc ou non.

Ces tests s'appuient également sur la distribution du Khi². Les résultats sont concordants, et indiquent que les données ne peuvent pas être supposées provenir d'un bruit blanc. Alors qu'un tri n'a aucune influence sur le test de Jarque-Bera, il en aurait un sur les autres tests qui sont adaptés aux séries temporelles.

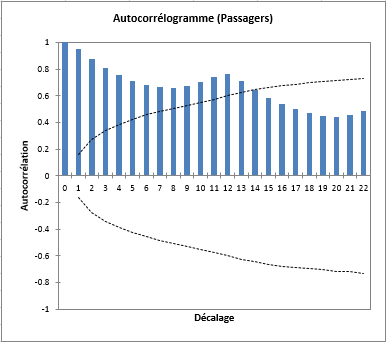
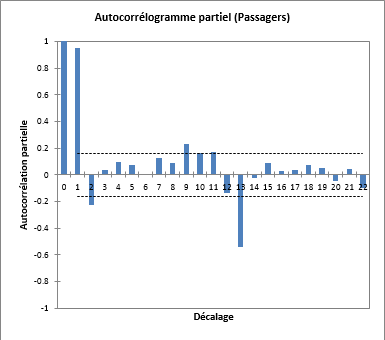
Dans le tableau ci-dessous sont affichées les fonctions descriptives de la série chronologique, et les deux diagrammes en bâtons correspondent à la fonction d'autocorrélation (FAC) et à la fonction d'autocorrélation partielle (FACP).

Les intervalles de confiance à 95% sont également affichés. Au niveau de l'autocorrélogramme, on identifie une autocorrélation d'ordre 1, ainsi qu'une saisonnalité de 12 mois.

Transformation d'une série temporelle

Dans le but d'augmenter la normalité des données, nous allons procéder à deux transformations successives :

Nous voulons d'abord stabiliser la variance de la série, Puis, retirer les autocorrélations significatives par une différenciation de la série. Cela peut être fait avec l'outil de transformation de séries temporelles.

Paramétrer la transformation d'une série temporelle

Pour activer la boîte de dialogue correspondante, choisissez la commande XLSTAT / XLSTAT-Time / Transformation de séries, ou cliquez sur le bouton correspondant de la barre d'outils XLSTAT-Time.

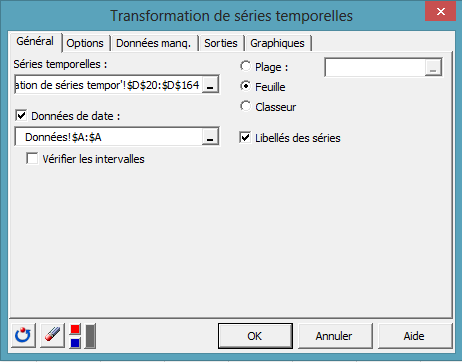
Sélectionnez les données sur la feuille Excel. La variable à transformer correspond ici à la série Passagers.

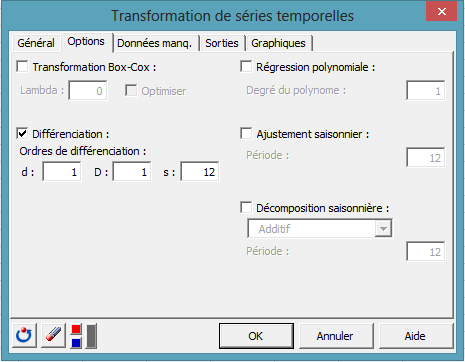
Après avoir sélectionné les données, activez l'option Box-Cox dans l'onglet Options.

Nous pourrions demander une transformation avec optimisation du paramètre lambda, mais nous décidons de fixer lambda à 0, ce qui revient à faire une transformation logarithmique de la série. Cette transformation est souvent efficace lorsque l'on souhaite supprimer une variabilité croissante,

Interpréter le résultat d'une transformation de série temporelle

D'abord, un tableau et deux graphiques apparaissent: l'un représentant le jeu de données d'origine et le deuxième représentant la transformation Box-Cox. Comme prévu, la transformation log a éliminé la variabilité croissante.

Ensuite, pour supprimer la tendance croissante et la composante saisonnière, nous décidons de faire une différenciation de la série. Dans la boîte de dialogue de transformation de série temporelle, nous sélectionnons les données transformées (Box-Cox).

La valeur de d est fixée à 1 pour retirer la tendance, et D et s sont fixés à 1 et 12 pour retirer la saisonnalité de douze mois.

Les calculs se lancent une fois que vous cliquez sur OK.

Interpréter le résultat d'une transformation de série temporelle

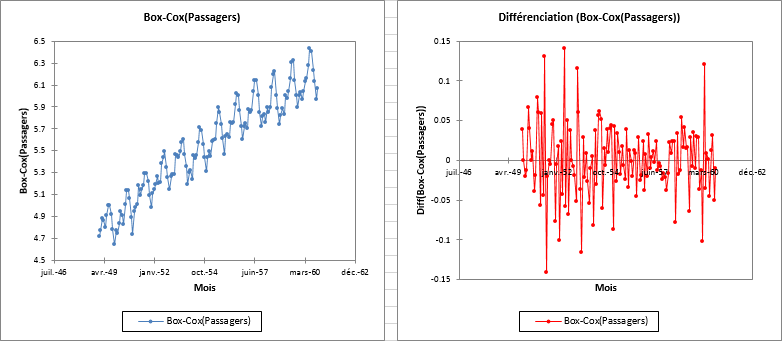
Les graphiques qui s'affichent montrent que les composantes tendancielle et saisonnière ont effectivement été éliminées.

Analyse descriptive des données chronologiques transformées

Dans le but de vérifier si les transformations ont permis de rendre la séries compatible avec un bruit blanc, nous devons réaliser une analyse descriptive de la série transformée.

Assurez-vous d'avoir bien sélectionné l'option Supprimer les observations dans l'onglet données manquantes car la correction de tendance et de saisonnalité a réduit le nombre de points.

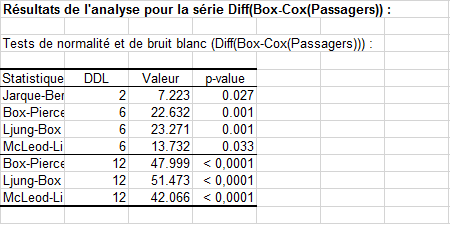
Le test de Jarque-Bera confirme que les séries sont plus proches d'une distribution normale : la probabilité est passée de 0,012 à 0,027. Cependant, les tests de bruit blanc indiquent que les transformations n'ont pas été suffisantes.

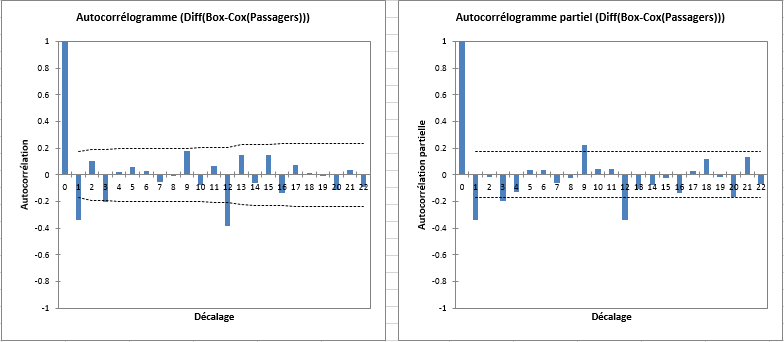
L'autocorrélogramme montre également que des composantes significatives au pas de temps 1 et 10 restent présentes. Une investigation plus poussée du processus générateur serait nécessaire pour mieux corriger la série.

Décomposition saisonnière de la série

Nous allons maintenant illustrer une seconde approche pour explorer notre série temporelle via l'option décomposition saisonnière de l'outil de transformation de séries temporelles. Nous repartons du jeu de données initial comme indiqué sur la figure qui suit.

Cette fois, nous choisissons l'onglet Décomposition saisonnière dans l'onglet Options. Nous choisissons le modèle multiplicatif car la série présente un comportement clairement compatible avec ce type de modèle. La période est réglée à 12 pour une périodicité annuelle avec des données mensuelles.

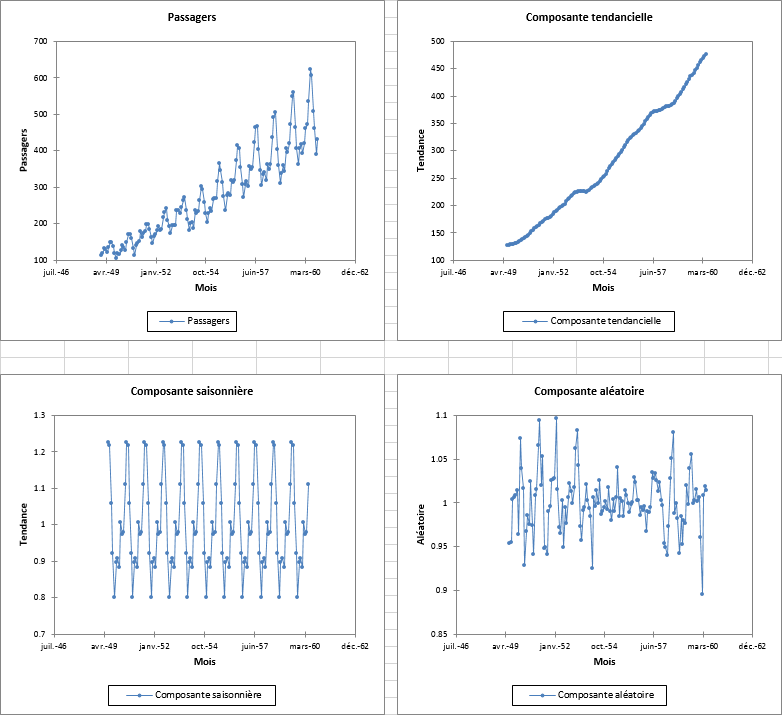
Une fois la décomposition calculée, nous obtenons un tableau et 4 graphiques présentant successivement la série initiale, la composante tendancielle, la composante saisonnière et la composante aléatoire. Les 3 dernières séries pouvant être multipliées entre elles pour reconstruire la première.

Nous souhaitons maintenant tester la stationnarité de la composante aléatoire. Pour cela, nous allons appliquer une transformation de Box-Cox sur cette composante aléatoire afin de la recentrer sur 0.

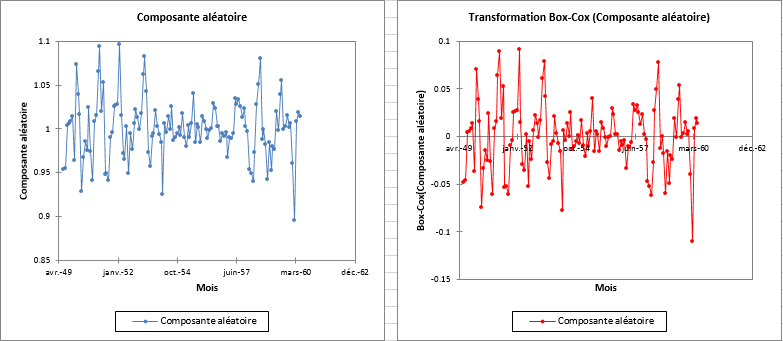
La figure ci-dessous montre le résultat de cette dernière transformation.

Nous lançons une nouvelle fois l'analyse descriptive sur notre série transformée.

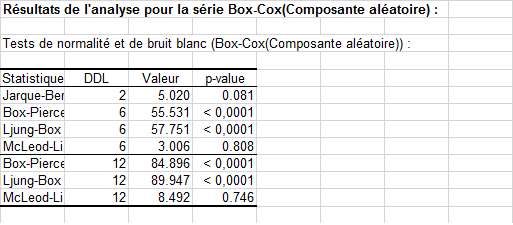
Cette fois, le test de Jarque-Bera ne permet pas de rejeter l'hypothèse d'une distribution normale.

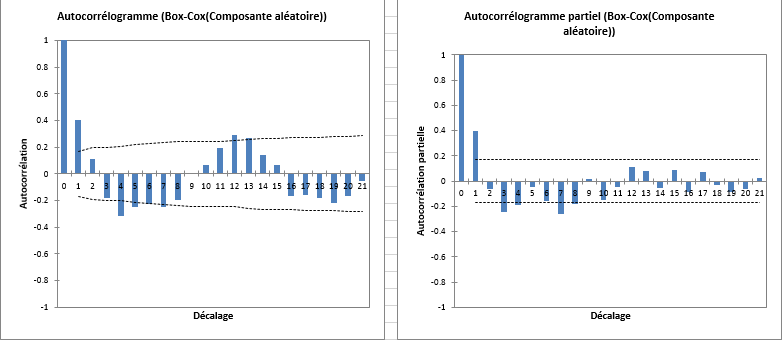
Cependant, nous pouvons tout de même identifier une composante saisonnière résiduelle, quoique diminuée, dans l'autocorrélogramme. Il semblerait qu'un travail d'analyse supplémentaire reste nécessaire pour identifier le processus générateur.