Régression logistique à 4 ou 5 paramètres dans Excel

Ce tutoriel explique comment calculer et interpréter une régression logistique à 4 ou 5 paramètres avec Excel en utilisant XLSTAT.

Régression logistique 4 ou 5 paramètres

La régression logistique à 4 ou 5 paramètres permet de modéliser l'effet d'une variable quantitative sur une variable réponse (densité optique, concentration, etc.), en utilisant le modèle logistique à 4 ou 5 paramètres, et en tenant éventuellement compte de contraintes liées à l'existence d'un échantillon standard.

Si aucun groupe ou un seul échantillon a été sélectionné, les résultats sont affichés pour le modèle choisi et pour cet échantillon. Si plusieurs sous-échantillons ont été définis (option sous-échantillons dans la boîte de dialogue), le modèle est d’abord ajusté à l’échantillon standard, puis chaque sous-échantillon est comparé à l’échantillon standard.

Jeu de données pour créer un modèle de régression à quatre paramètres

Dans ce tutoriel, nous étudions un cas médical dans lequel une molécule active est injectée à différentes concentrations fixées, et l'on mesure en réponse la concentration de certaines cellules dans le sang.

Paramétrer une régression logistique à quatre paramètres dans XLSTAT

Pour activer la boîte de dialogue de la régression logistique à quatre paramètres, lancez XLSTAT, puis sélectionnez la commande Dose / Régression logistique à 4/5 paramètres et courbes parallèles.

Une fois que vous avez cliquez sur la commande, la boîte de dialogue apparaît.

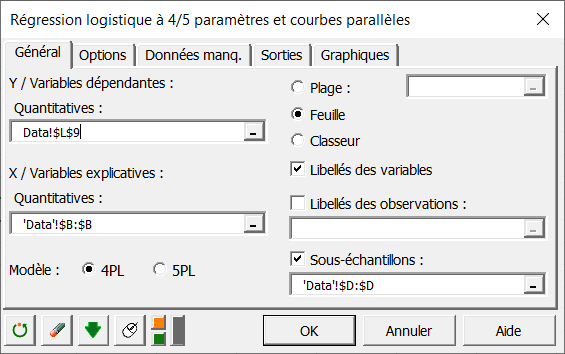
Sélectionnez alors les données dans la feuille Excel. Pour la Variable dépendantes Y, choisissez les données de la colonne C : Conc, qui représente la concentration des cellules dans le sang. La variable explicative est le logarithme de la concentration de molécules injectées qui est dans la colonne B (Log(Dose)).

Vous devez aussi choisir d'activer l'option Libellés des variables, car les colonnes contiennent des titres. Enfin renseignez le champ Sous-échantillon en sélectionnant le Cas qui se trouve dans la colonne D.

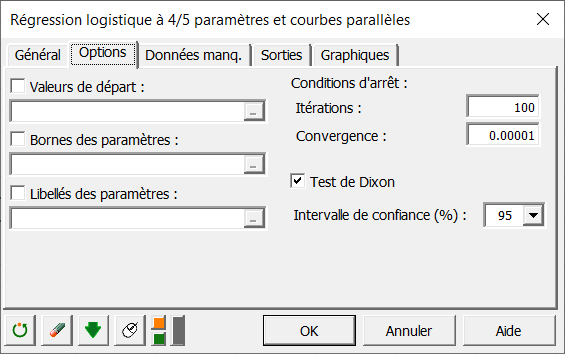
Dans l'onglet Options, désélectionnez le test de Dixon car il ne devrait pas y avoir d'outliers (échantillons aberrants) dans ce jeu de données.

Lancez les calculs en cliquant sur le bouton OK. Les résultats apparaissent dans une nouvelle feuille Excel.

Interpréter les résultats d'une régression logistique à quatre paramètres

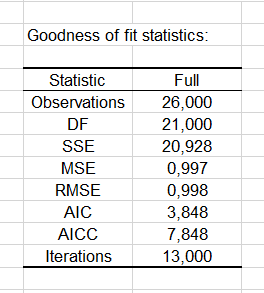
Les premiers résultats concernent l'échantillon standard. Les coefficients d'ajustement du modèle sont bons.

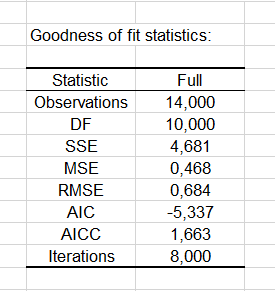
Les paramètres du modèle sont présentés ci-dessous.

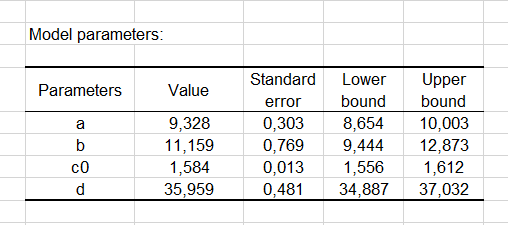
Finalement la courbe du modèle peut aussi être analysée.

Des graphiques supplémentaires sont également affichés pour une analyse des résidus. 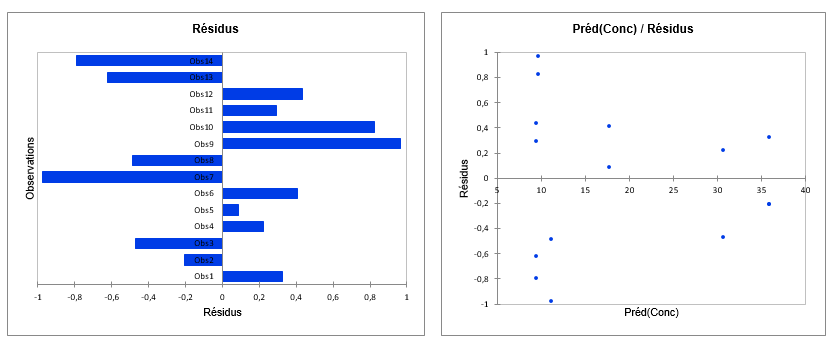Une fois ces premières sorties affichées, on s'intéresse à l'effet de deux sous-échantillons.

L'un des résultats importants de cette analyse est le test de Fisher pour tester le parallélisme entre les courbes. Regardez la valeur de la p-value.

L'hypothèse H0 peut être rejetée, les courbes ne sont donc pas parallèles. Il y a donc une différence significative entre les deux échantillons.

Cependant les coefficients d'ajustement du modèle sont bons. Le modèle rend donc bien compte de la différence entre les échantillons grâce aux paramètres c1 et c2.

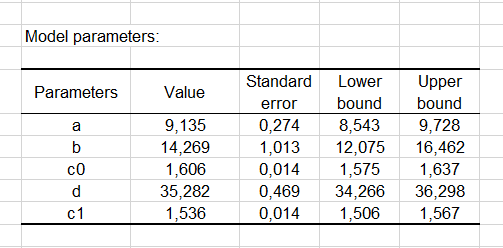
Les paramètres du modèle sont présentés ci-dessous. On peut voir que les coefficients c1 et c2 présentent une variation faible.

Le graphique qui se trouve après les résultats numériques, les courbes logistiques parallèles, permet de visualiser les courbes des régressions et la différence entre les deux échantillons.

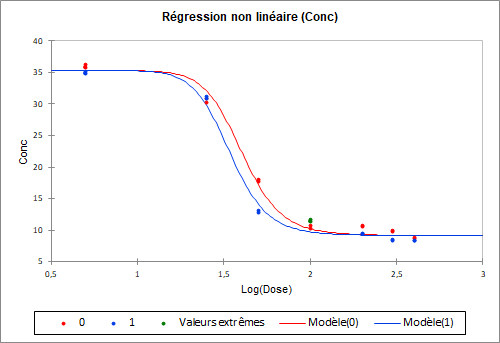
Les différences entre les deux échantillons sont les plus importantes pour un Log(Dose) entre 1.3 et 2.