Stichproben für klinische Versuche in Excel
Dieses Tutorium zeigt Ihnen, wie Sie einen Stichprobenumfang für einen klinischen Versuch in Excel mithilfe der Statistiksoftware XLSTAT berechnen.## Absicht dieses Tutoriums
Dieses Tutorium zielt darauf ab, zu zeigen, wie die notwendige Stichprobengröße in klassischen klinischen Studien geschätzt werden kann. Bei der Organisation einer Studie stellt sich als erstes die Frage, wie viele Patienten in die Studie eingeschlossen werden müssen, um statistisch gültige Ergebnisse zu erzielen. Es können drei Typen von Studien untersucht werden:- Äquivalenztests: Bei einem Äquivalenztest soll demonstriert werden, dass eine neue Therapie weder besser noch schlechter als eine bestehende Therapie ist.
- Überlegenheitstests: Bei einem Überlegenheitstest soll demonstriert werden, dass eine Therapie besser als eine andere ist.
- Nicht-Unterlegenheitstests: Bei einem Nicht-Unterlegenheitstest soll gezeigt werden, dass eine neue Therapie nicht schlechter als eine bestehende Therapie ist.
Diese Tests können auf eine binäre Variable oder eine kontinuierliche Variable angewendet werden. Wir geben drei Beispiele für jede dieser Versuche. Sie finden die Ergebnisse## Datensatz für die Berechnung der notwendigen Stichprobengröße
Eine Excel-Mappe mit den Ergebnissen dieses Beispiels kann hier heruntergeladen werden.## Einrichten der Berechnung den notwendigen Stichprobenumfang für einen klinischen Versuch
Nach dem Öffnen von XLSTAT klicken Sie auf das Symbol Mächtigkeit und wählen Sie klinische Versuche.
 Nach dem Klicken des entsprechenden Buttons erscheint das Dialogfenster.## Überlegenheitstest
Nach dem Klicken des entsprechenden Buttons erscheint das Dialogfenster.## Überlegenheitstest
Eine neue Therapie wurde erhalten, deren erwartete Ergebnisse an Patienten besser sein sollten als bei der derzeitigen Therapie. Wir möchten die Stichprobengröße ermitteln, die notwendig ist, um die Nullhypothese abzulehnen, dass beide Therapien denselben Effekt haben.
Das Ergebnis ist die Tatsache, ob ein Patient geheilt ist oder nicht. Dies ist eine binäre Variable. Wir nehmen an, dass die Kontrollgruppe (mit der ältesten Therapie) eine Genesung von 60 % aufweist, und dass die Behandlungsgruppe (mit der neuen Therapie) eine Genesung von 70 % aufweist. Wir möchten die notwendige Stichprobengröße für ein Niveau von 5 % und eine Mächtigkeit von 0,9 schätzen.
Sie müssen dann das Ziel Finden Sie den Stichprobenumfang und danach den Überlegenheitstest und die binäre Variable auswählen. Alpha liegt bei 0,05. Die gewünschte Mächtigkeit beträgt 0,9. Der Erfolgsanteil für die Kontrollgruppe liegt bei 60 % und der Erfolgsanteil für die behandelte Gruppe liegt bei 70 %. Es gibt keinen Kreuzungspunkt.
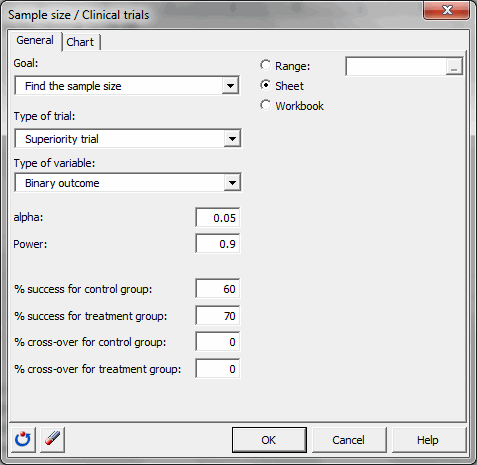 Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Überlegenheitstest
Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Überlegenheitstest
Die erste Tabelle zeigt die Berechnungsergebnisse und eine Interpretation der Ergebnisse an.
 Wir können sehen, dass 945 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 473 Patienten.
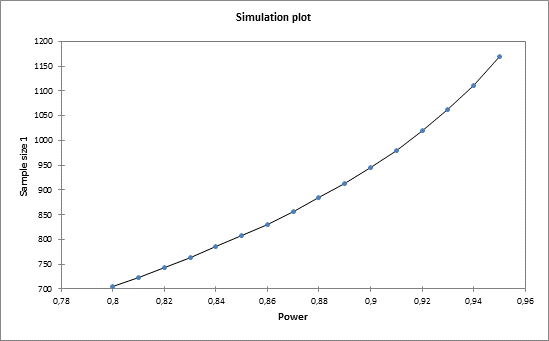
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
Wir können sehen, dass 945 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 473 Patienten.
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
 ## Äquivalenztest
## Äquivalenztest
Eine neue Therapie wurde erhalten, die weitaus weniger Nebenwirkungen hat als die klassische Therapie. Wir möchten sicher sein, dass beide Therapien gleichwertig sind. Hierzu möchten wir testen, dass beide Therapien im selben Ergebnisbereich liegen.
Wir verwenden Äquivalenztests. Eine Äquivalenzgrenze muss definiert werden. In unserem Fall definieren wir eine Äquivalenzgrenze von 10 %.
Das Ergebnis ist die Tatsache, ob ein Patient geheilt ist oder nicht. Dies ist eine binäre Variable. Wir nehmen an, dass die Kontrollgruppe (mit der ältesten Therapie) und die behandelte Gruppe (mit der neuen Therapie) eine Genesung von 60% aufweisen. Wir möchten die notwendige Stichprobengröße für ein Niveau von 5 % und eine Mächtigkeit von 0,9 schätzen.
Sie müssen dann das Ziel Finden Sie den Stichprobenumfang auswählen und danach den Überlegenheitstest und die binäre Variable auswählen. Alpha liegt bei 0,05. Die gewünschte Mächtigkeit beträgt 0,9. Der Erfolgsanteil für beide Gruppen liegt bei 60 % und die Äquivalenzgrenze bei 10 %.
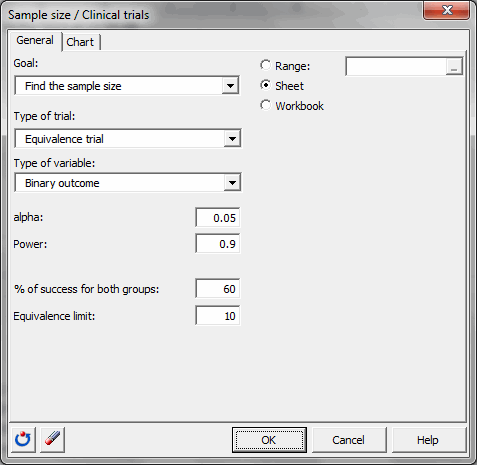 Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Äquivalenztest
Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Äquivalenztest
Die erste Tabelle zeigt die Berechnungsergebnisse und eine Interpretation der Ergebnisse an.
 Wir können sehen, dass 1038 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 519 Patienten.
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
Wir können sehen, dass 1038 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 519 Patienten.
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
 ## Nicht-Unterlegenheitstest
## Nicht-Unterlegenheitstest
Eine neue Therapie wurde erhalten, die weniger Nebenwirkungen hat als die klassische Therapie. Wir möchten sicher sein, dass die neue Therapie einen mindestens gleichen oder geringfügig geringeren Effekt hat als die aktuelle Therapie. Hierzu möchten wir testen, ob die neue Therapie besser oder geringfügig schlechter ist als die ursprüngliche Therapie ist.
Wir verwenden Nicht-Unterlegenheitstests. Eine Nicht-Unterlegenheitsgrenze muss definiert werden. In unserem Fall definieren wir eine Nicht-Unterlegenheitsgrenze von 8 %.
Das Ergebnis ist die Tatsache, ob ein Patient geheilt ist oder nicht. Dies ist eine binäre Variable. Wir nehmen an, dass die Kontrollgruppe (mit der ältesten Therapie) eine Genesung von 70% aufweist, und dass die Behandlungsgruppe (mit der neuen Therapie) eine Genesung von 75% aufweist. Wir möchten die notwendige Stichprobengröße für ein Niveau von 5 % und eine Mächtigkeit von 0,9 schätzen.
Sie müssen dann das Ziel Finden Sie den Stichprobenumfang und danach den Nicht-Unterlegenheitstest und die binäre Variable auswählen. Alpha liegt bei 0,05. Die gewünschte Mächtigkeit beträgt 0,9. Der Erfolgsanteil für die Kontrollgruppe liegt bei 70 % und der Erfolgsanteil für die behandelte Gruppe liegt bei 75 %. Die Nicht-Unterlegenheitsgrenze liegt bei 8.
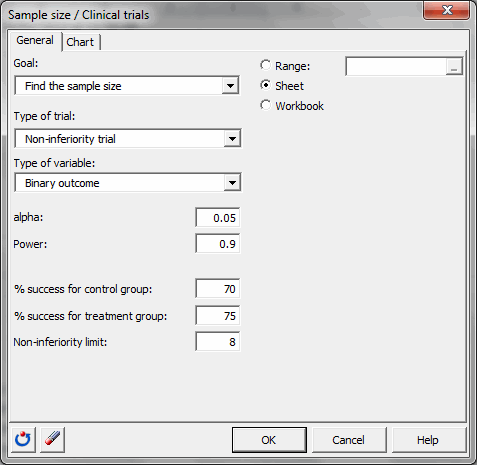 Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Nicht-Unterlegenheitstest
Sobald Sie auf den Button OK geklickt haben, erfolgen die Berechnungen und die Ergebnisse werden angezeigt.#### Ergebnisse der Berechnung der notwendigen Stichprobengröße für einen Nicht-Unterlegenheitstest
Die erste Tabelle zeigt die Berechnungsergebnisse und eine Interpretation der Ergebnisse an.
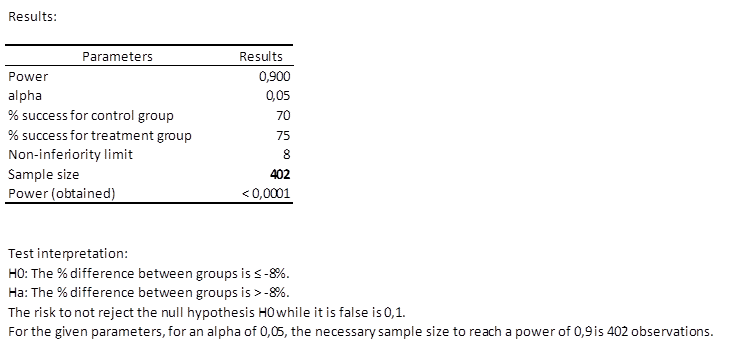 Wir können sehen, dass 402 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 201 Patienten.
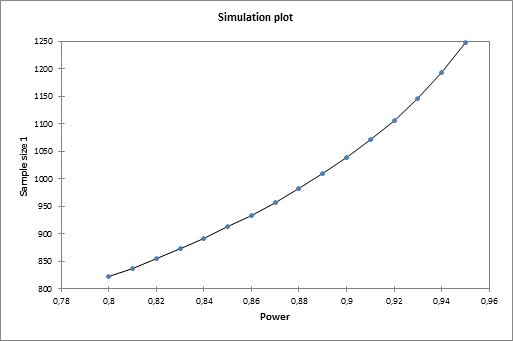
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
Wir können sehen, dass 402 Patienten notwendig sind, d. h. zwei Gruppen mit mindestens 201 Patienten.
Das Simulationsdiagramm liefert Ihnen weitere Informationen über die Entwicklung der Stichprobengröße in Bezug auf die Mächtigkeit.
 ## Schlussfolgerungen
## Schlussfolgerungen
XLSTAT bietet Ihnen die Möglichkeit, die erforderliche Stichprobengröße für viele Arten von Versuchen zu erreichen. Wir haben gesehen, dass Nicht-Unterlegenheitstests weniger restriktiv sind als die anderen, aber auch kontroverser. XLSTAT bietet Ihnen die Möglichkeit, die Mächtigkeit und notwendige Stichprobengröße zu ermitteln, wenn die abhängige Variable kontinuierlich ist, und viele Simulationsdiagramme zu repräsentieren.
Was this article useful?
- Yes
- No
 Help Center
Help Center